КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теорема. абсолютное ускорение точки геометрически складывается из переносного, относительного и Кориолисова ускорений.
,
где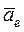 
– переносное ускорение; 
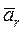– относительное ускорение; 
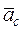– ускорение Кориолиса: 
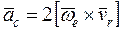. модуль ускорения Кориолиса можно найти по формуле
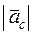=2| ωe |∙|vr |∙sinβ, где β – угол между векторами 
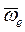и 
. в рассматриваемом случае этот угол равен 90º, т. к. вектор угловой скорости направлен перпендикулярно плоскости рисунка от нас. Для определения направления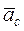 
можно пользоваться правилом векторного умножения, или правилом Жуковского: для определения направления ускорения Кориолиса надо спроецировать вектор относительной линейной скорости на плоскость перпендикулярную оси переносного вращения и повернуть эту проекцию в этой плоскости на угол 90° в направлении переносной угловой скорости.
Ускорение Кориолиса равно нулю, если:
1) 
= 0 ; т.е. переносное движение будет поступательным;
2) 
= 0 ; т.е. точка неподвижна по отношению к подвижной системе отсчета;
3. 
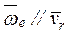; т.е. точка движется параллельно оси переносного вращения.
Дата добавления: 2015-04-15; просмотров: 198; Мы поможем в написании вашей работы!; Нарушение авторских прав |