
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Скаляры и векторы
КИНЕМАТИКА И ДИНАМИКА ПОСТУПАТЕЛЬНОГО
И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Методические указания по решению задач
Омск 2004
Составители: Н.В. Бердинская
В.О. Нижникова
С.С. Ясько
Рассматриваются теоретические вопросы разделов кинематики и динамики поступательного и вращательного движений. После теоретических вопросов приведены примеры решения задач по данной теме и в заключении представлены семь блоков задач по тридцать вариантов в каждом блоке для самостоятельного решения в качестве домашних заданий.
Предназначены для студентов дневного и вечернего обучения всех технических специальностей.
Печатается по решению редакционного издательского совета Омского государственного технического университета.
Механика материальной точки
Скаляры и векторы
В физике широко используются скалярные и векторные величины.
Скалярной называется величина, каждое значение которой выражается одним числом в любой системе координат (длина, время, масса и т.п.).
Вектором называется величина, определяемая числовым значением и направлением в пространстве (скорость, сила, напряженность и т.п.).
Длина вектора, измеренная в определенном масштабе, называется модулем вектора.
Любой вектор можно представить в виде произведения его модуля на единичный вектор  .
.
Единичные векторы, направленные вдоль координатных осей, принято обозначать:  ;
;  ;
;  .Они называются ортами.
.Они называются ортами.
Пусть известен угол α между некоторой осью Ох и вектором  . Опустим перпендикуляр из конца вектора
. Опустим перпендикуляр из конца вектора  на эту ось (рис. 1.1.).
на эту ось (рис. 1.1.).
 |




 К х
К х
Рис. 1.1
Величина  называется проекцией вектора
называется проекцией вектора  на ось Ох. Знак проекции определяется знаком cosα, а ее численное значение равно длине отрезка ОК.
на ось Ох. Знак проекции определяется знаком cosα, а ее численное значение равно длине отрезка ОК.
Если в пространстве задана прямоугольная система координат, то проекции вектора  на координатные оси обозначаются
на координатные оси обозначаются  ,
,  ,
,  . (рис. 1.2.)
. (рис. 1.2.)
 у
у










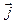



 х
х



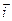

 z
z

Рис. 1.2
Любой вектор  может быть представлен в виде суммы трех векторов:
может быть представлен в виде суммы трех векторов:
 . (1.1)
. (1.1)
Модуль вектора  в этом случае равен
в этом случае равен
 . (1.2)
. (1.2)
Суммой двух векторов  и
и  называется вектор
называется вектор  =
=  +
+ 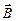 .
.  – результирующий вектор;
– результирующий вектор;  и
и  – составляющие векторы (рис. 1.3).
– составляющие векторы (рис. 1.3).








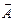

Рис. 1.3
Для определения результирующего вектора  перемещаем вектор
перемещаем вектор  парал-лельно самому себе так, чтобы его начало совпадало с концом вектора
парал-лельно самому себе так, чтобы его начало совпадало с концом вектора  . Из начала вектора
. Из начала вектора  к концу вектора
к концу вектора  проводим вектор
проводим вектор  .
.
В физике широко используются два вида произведений векторов: скалярное и векторное.
Скалярное произведение двух векторов  и
и  - это скалярная величина, численно равная произведению модулей этих векторов на косинус угла между ними:
- это скалярная величина, численно равная произведению модулей этих векторов на косинус угла между ними:
 .
.
Векторным произведением векторов  и
и  является вектор
является вектор  , модуль которого равен произведению модулей этих векторов на синус угла между ними.
, модуль которого равен произведению модулей этих векторов на синус угла между ними.
Направление вектора  перпендикулярно плоскости, в которой лежат векторы
перпендикулярно плоскости, в которой лежат векторы  и
и  , так, что если смотреть с его конца, то кратчайший поворот от
, так, что если смотреть с его конца, то кратчайший поворот от  к
к  будет происходить против часовой стрелки (рис. 1.4).
будет происходить против часовой стрелки (рис. 1.4).


 |






Рис. 1.4
Дата добавления: 2015-04-15; просмотров: 228; Мы поможем в написании вашей работы!; Нарушение авторских прав |