Вращательное движение абсолютно твердого тела вокруг неподвижной оси и его кинематические характеристики

Всякое сложное движение твердого тела можно разбить на два простых: поступательное и вращательное.

Рассмотрим вращательное движение твердого тела вокруг закрепленной оси. Это такое движение, при котором все точки тела движутся по окружностям с центрами, лежащими на оси вращения.

] [

] [

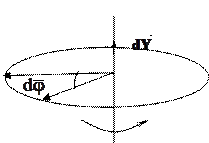
Рис. 2.1

Основными кинематическими характеристиками такого движения являются следующие:

1. Угловое перемещение – это векторная физическая величина, численно равная углу поворота твердого тела , направленная вдоль оси вращения и связанная с направлением вращения правилом правого винта (рис. 2.1).

2. Угловая скорость - это векторная физическая величина, численно равная и совпадающая по направлению с угловым перемещением, совершаемым за одну секунду:

. (2.1)

Если задана зависимость угловой скорости от времени, то можно найти угловое перемещение, совершаемое телом за определенный промежуток времени:

,

,

. (2.2)

3. Угловое ускорение.

Быстрота изменения угловой скорости характеризуется угловым ускорением:

. (2.3)

Угловым ускорением называется физическая величина, численно равная и совпадающая по направлению с приращением угловой скорости за единицу времени.

Зная зависимость углового ускорения от времени, можно найти изменение угловой скорости за определенный промежуток времени

(2.4)

Скорости, с которыми точки твердого тела движутся по окружностям, называются линейными скоростями. Линейная скорость точек зависит от их расстояния до оси вращения, и связана с угловой скоростью твердого тела соотношением

(2.5)

Изменение линейной скорости характеризуется линейным ускорением, которое складывается из тангенциального и нормального ускорений.

Модуль тангенциального ускорения связан с модулем углового ускорения соотношением:

(2.6)

Модуль нормального ускорения связан с модулем угловой скорости соотношением:

(2.7)