Кинематика материальной точки. Все тела имеют определенные размеры и форму

Все тела имеют определенные размеры и форму. Но в некоторых случаях размерами тела можно пренебречь.

Тело, размерами которого при изучении его движения можно пренебречь, называется материальной точкой.

Для описания движения материальной точки необходимо указать систему отсчета, относительно которой движение происходит. Система отсчета включает в себя тело отсчета, связанную с ним систему координат и прибор для измерения времени.

Положение точки в пространстве можно определить, задав ее координаты (x, y, z), или радиус – вектор, т.е. вектор, проведенный из начала координат в рассматриваемую точку (рис. 1.5), и выражается соотношением:

А

х

(Рис. 1.5)

. (1.3)

Модуль радиус-вектора:

. (1.4)

Если материальная точка перемещается в пространстве, то ее радиус – вектор с течением времени изменяется:

. (1.5)

Это соотношение называется уравнением движения.

При движении материальная точка описывает линию.

Линия, которую описывает точка в данной системе координат, называется траекторией.

В зависимости от формы траектории различают прямолинейное и криволинейные движения.

При движении точки из положения I в положение II (рис. 1.6) радиус – вектор меняется от до .

Рис. 1.6

Величина называется приращением радиус-вектора, или вектором перемещения; т.е. вектор перемещения – это вектор, проведенный из начальной точки траектории в конечную.

Расстояние, пройденное материальной точкой вдоль траектории, называется длиной пути (S).

Движение материальной точки характеризуется ее скоростью. Это векторная физическая величина, численно равная и совпадающая по направлению с перемещением, совершаемым за единицу времени.

В общем случае неравномерного криволинейного движения используются понятия средней и мгновенной скоростей.

Мгновенная скорость определяется выражением

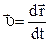. (1.6)

Ее модуль

. (1.7)

Направлена мгновенная скорость по касательной к траектории (рис. 1.7).

Пользуясь соотношением (1.6), можно найти приращение радиус-вектора:

,

,

,

. (1.8)

Пользуясь выражением (1.7), можно найти путь S, пройденный материальной точкой за время :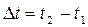

,

,

. (1.9)

Средняя скорость определяется равенством

и совпадает по направлению с вектором перемещения (рис. 1.7).

1

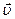
2

Рис. 1.7

Изменение скорости характеризуется ускорением.

Ускорение – это векторная физическая величина, численно равная и совпадающая по направлению с приращением скорости за единицу времени.

Используются понятия мгновенного и среднего ускорений.

Мгновенное ускорение определяется соотношением:

. (1.10)

Соотношение (1.10) позволяет найти зависимость скорости от времени:

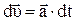, (1.11)

, (1.12)

или приращение скорости за время

,

. (1.13)

При неравномерном криволинейном движении изменяются величина и направление скорости. В этом случае полное ускорение представляет собой сумму двух ускорений – тангенциального и нормального :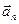

(1.14)

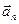
Рис. 1.8

Тангенциальное ускорение характеризует быстроту изменения модуля скорости. Его модуль равен:

(1.15)

Оно направлено по касательной к траектории (рис. 1.8).

Нормальное ускорение характеризует быстроту изменения скорости по направлению. Его модуль равен:

, (1.16)

R – радиус кривизны траектории в рассматриваемой точке. Направлено нормальное ускорение к центру кривизны траектории (рис. 1.8).

Модуль полного ускорения

. (1.17)

Одним из видов движения тела является прямолинейное движение с постоянным ускорением . Оно называется равнопеременным.

Такое движение описывается уравнениями:

, (1.18)

. (1.19)