Касательное и нормальное ускорение точки

Вектор ускорения a точки лежит в соприкасающейся плоскости P n и определяется двумя проекциями 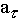и a_n(a_b = 0):

• проекция ускорения точки на касательную равна первой производной от алгебраической скорости или второй производной от криволинейной координаты точки по времени:

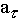= d / dt = d²s /dt² или = = .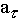

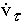• проекция ускорения на главную нормаль равна квадрату скорости, деленному на радиус кривизны траектории в данной точке кривой:

a_n = v² / .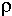

Величины 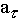и a_n соответственно называют касательным и нормальнымускорениями точки.

Вектор ускорения a является векторной суммой касательной составляющей , напраленной вдоль касательной P , и нормальной составляющей a_n, направленной вдоль главной нормали Pn:

a = + a_n.

При этом составляющая может быть направлена или в положительном, или в отрицательном направлении оси P в зависимости от знака проекции 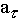, а составляющая a_n будет всегда направлена в сторону вогнутости кривой, так как проекция a_n 0.

Так как эти составляющие взаимно перпендикулярны, то модуль вектораa определяется по формуле:

a = ( ² + a_n² ) .

Рассмотрим теперь геометрическую характеристику траектории точки, называемую радиусом кривизны .

Радиус кривизны кривой в какой-либо ее точке равен радиусу окружности, которая наилучшим образом аппроксимирует по сравнению с другими окружностями участок кривой из малой окрестности рассматриваемой точки. Величина, обратная радиусу кривизны, называетсякривизной кривой k = 1 / 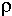в данной точке.

В частности, для окружности радиус кривизны одинаков во всех ее точках и равен ее радиусу: 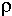= R (кривизна окружности k = 1 / R); для прямой радиус кривизны 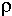= (кривизна прямой k = 0).

Рассмотрим условия, при которых касательное и нормальное ускорения обращаются в нуль.

• Касательное ускорение равно нулю, если 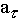= d / dt = 0.
  Это условие выполняется, если все время v = | | = const, то есть при равномерном движении точки по траектории любой формы.
  Касательное ускорение обращается в нуль также в те моменты времени, в которые алгебраическая скорость достигает экстремума, например максимума или минимума.
• Нормальное ускорение равно нулю, если a_n = v² / 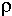= 0.
  Это условие выполняется, если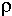 = , то есть при прямолинейном движении точки. При движении точки по криволинейной траектории 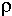= в точках перегиба, в которых происходит изменение выпуклости траектории на вогнутость, и наоборот.
  Нормальное ускорение обращается в нуль также в моменты времени, в которые v = 0, то есть в моменты изменения направления движения точки по траектории.