Теорема о сложении ускорений

Ускорение любой точки тела в плоском движении равно геометрической сумме ускорения точки тела в поступательном движении совместно с полюсом и ускорения вращения точки вокруг полюса во вращательном движении тела вокруг полюса.

Дифференцируя по времени выражение (2), получаем

В последнем выражении вектор углового ускорения тела ε направлен по оси вращения тела, совпадающей с осями Az* и Az₁ , так как при плоском движении вектор ω не изменяет своего направления в пространстве, двигаясь параллельно самому себе (рис. 88). То есть распределение ускорений в базовой системе координат такое же, как и при вращении тела вокруг неподвижной оси. На рис. 88 показан случай, когда ускоренное вращение происходит против хода часов, а остальные оси базовой и связанной с телом систем координат не показаны.

Очевидно, что a_A является ускорением полюса или ускорением поступательного движения базовой системы координат и тела совместно с полюсом. Согласно векторным формулам для ускорений точек тела при вращательном движении (см. п. 33) вектор касательного ускорение вращения вокруг полюса равен

(7)

он перпендикулярен радиусу вращения AB и направлен в сторону углового ускорения, а его величина равна

(8)

Вектор нормального ускорения равен

(9)

он направлен по радиусу вращения AB от точки B к полюсу A, а его величина равна

(10)

При вычислении величин векторов в формулах (8) и (10) учитывалось, что векторы ρ и V_BA лежат в плоскости движения, а векторы ω и ε перпендикулярны ей (рис.88).

Подставляя формулы (7) и (9) в выражение для a_B , получаем

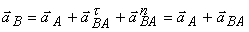
(11)

и теорема доказана.

Отметим, что теорема о сложении ускорений точек тела в плоском движении часто используется для решения задач. Ускорения могут быть найдены в двух основных случаях, когда: 1) расстояние от полюса до мгновенного центра скоростей в процессе движения остается постоянной величиной; 2) ускорение одной точки тела (полюса) и траектория второй точки тела известны.

25.) Модуль и направление поворотного ускорения