
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Нелинейные УУН в форме баланса мощностей в полярной системе координат
Такая запись УУН удобна для анализа режима генераторных узлов, потому что в этих узлах, как правило, вместо реактивной мощности задается модуль напряжения. Для получения новой формы УУН применяется показательная форма записи комплексов:
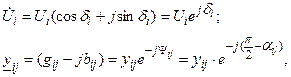
| (2.22) |
| Рис. 2.10. Угол проводимости |
где Ui - модуль напряжения узла i; δi -сдвиг по фазе напряжения узла i, по отношению к балансирующему. Угол  комплекса проводимости
комплекса проводимости  , как правило, представляется через угол
, как правило, представляется через угол 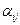 , дополняющий
, дополняющий  до
до  (рис. 2.10)
(рис. 2.10)
 .
.
После подстановки (2.22) в (2.20) получаем
 .
.
Данное выражение преобразуется к виду
 .
.
Используя хорошо известные тригонометрические соотношения:
cos(-x ) = cos x; sin(-x) = -sin x; cos(p/2 + x) =-sin x;
sin(x + p/ )= cos x; cos(x- p/2) =sinx; sin(x - p/2)=-cos x,
получаем


Приравнивая действительные и мнимые составляющие, получаем уравнения баланса мощностей в полярной системе координат:
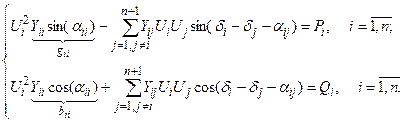
| (2.23) |
В выражении (2.23) Pi и Qi - активная и реактивная мощности нагрузки в узле i.
При анализе установившихся режимов в реальных энергосистемах узлы разделяются на два класса:
а) так называемые нагрузочные узлы, в которых задаются Pi и Qi, а неизвестными параметрами являются модули Ui и углы δi напряжений;
б) генераторные узлы (узлы с фиксированным модулем напряжения), в них задаются Pi и Ui, и диапазон изменения реактивной мощности (Qmin, Qmax), а неизвестными параметрами являются δi и Qi. В этом случае для сети, содержащей n узлов без балансирующего, достаточно решить первые n (а не 2n уравнений, как в случае а) тригонометрических уравнений системы (2.23) относительно углов. Искомые реактивные мощности определяются однозначно из второй половины уравнений (2.23). Таким образом, система неизвестных(δi,Qi) позволяет сократить размерность решаемой задачи.
В качестве примера рассмотрим сеть переменного тока, рис. 2.6, где в узлах заданы не токи, а мощности S1=30+j10, S2=-(20+j20). Проводимости ветвей, а также –Y11 представлены в табл. 2.1
Таблица 2.1
| Связь | Y | |Y| | -ψ | α |
| 1-б | 1-1i | 1,41 | -45,00 | 45,00 |
| 1-2 | 1-2i | 2,24 | -63,43 | 26,57 |
| –Y11 | (2-3i) | 3,61 | -56,31 | 33,69 |
В результате система УУН в полярной системе координат имеет вид

В результате можно отметить, что система УУН может быть записана как в линейной так и нелинейной форме, как в форме баланса токов и как в форме баланса мощностей. Количество уравнений и переменных для сети переменного тока увеличивается вдвое.
Дата добавления: 2015-04-16; просмотров: 355; Мы поможем в написании вашей работы!; Нарушение авторских прав |