Определитель матрицы

Одной из числовых характеристик квадратной матрицы является ее определитель.

Для вычисления определителя второго и третьего порядка обычно используют правило Саррюса (схема диагоналей и треугольников), согласно которому

(3.1)

Первое слагаемое, входящих в правую часть со знаком плюс, есть произведение элементов главнойдиагонали матрицы А, следующие два — произведение элементов, лежащих на параллели к этой диагонали, и элемента из противоположного угла матрицы. Слагаемые, входящие в (3.1) со знаком минус, строятся таким же образом, но относительно побочной диагонали. Данному правилу соответствуют схемы, облегчающие вычисление слагаемых:

.

Для определителя второго порядка

. Пример.

Однако чаще всего определитель вычисляется по формуле разложения по строке или столбцу. При этом необходимо ввести некоторые понятия.

Минором элемента определителя порядка n называется определитель порядка , получаемый из исходного определителя путем вычеркивания строки i и столбца j, на пересечении которых стоит указанный элемент .

Алгебраическим дополнением элемента определителя порядка n будем называть его минор, взятый со знаком плюс, если сумма индексов строки и столбца четна, и со знаком минус, если эта сумма нечетна:

Определитель равен сумме произведений элементов какой - либо его строки (какого - либо столбца) на соответствующие алгебраические дополнения элементов этой строки (этого столбца).

,

где - элементы строки i; - алгебраическое дополнение элемента ; 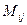- минор – определитель матрицы, полученной из исходной вычеркиванием строки i и столбца j. В частности, для определителя третьего порядка