Матричная запись линейных УУН

Записанная в матричной форме система УУН для сети постоянного тока имеет вид (2.4) , для сети переменного тока все представленные в этом уравнении величины являются комплексными

(3.4)

Однако, как это было отмечено ранее, в практических расчетах предпочтение отдается действительной системе линейных уравнений. В прямоугольной системе координат УУН имеют вид (2.14)

(3.5)

Данную блочную форму системы УУН интересно получить путем матричных преобразований. Принимая во внимание соотношения

выполняются следующие матричные преобразования

Разделяя действительную и мнимую составляющие, получаем

Используя блочную запись матриц, эту систему можно представить в виде (3.5) .

3.4. Прямые методы решения СЛУ

Методы решения СЛУ можно разделить на две группы:

Прямые методы. Вектор неизвестных определяется за определенное количество операций, число которых может быть определено заранее. Для решения СЛУ достаточно найти матрицу А^-1 и представить решение в форме: .

Итерационные методы. Здесь вычисляется последовательность ^{`</sup>X<sup>(1)</sup>,<sup>`}X⁽²⁾, ...`X<sup>(k)</sup> приближений переменных к решению, начиная от некоторого<sup>`</sup>X⁽⁰⁾,так что предел стремится к решению :

.

Итерационные методы нашли широкое применение для решения систем нелинейных уравнений. Для систем линейных уравнений они используются редко. Здесь чаще используются специализированные прямые методы.

Теорема Кронекера – Капелли

Для того чтобы система линейных уравнений являлась разрешимой, необходимо и достаточно, чтобы ранг расширенной матрицы этой системы был равен рангу её основной матрицы.

Формулы Крамера

Решение системы линейных уравнений 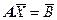может быть получено через расчет определителей.

,

(3.6)

где Δ - определитель матрицы , -определитель матрицы, полученной заменой столбца k матрицы коэффициентов на столбец свободных членов .

Доказательство представленного выражения представляет интерес как один из приемов работы с массивами.

Умножим каждое уравнение i СЛУ

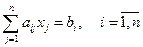
на и просуммируем все уравнения

.

Обратим внимание, что правая часть представляет . В левой части уравнения выполним замену порядка суммирования

Поскольку для всех j¹k (скалярное произведение столбца j на алгебраические дополнения другого столбца k), получаем: , что и требовалось доказать .

Формула Крамера находит широкое применение для ручных расчетов СЛУ относительно небольшого (2-3) порядка.

3.5. Метод Гаусса

Наибольшее распространение для решения систем уравнений получил метод Гаусса. Основная идея его заключается в последовательном исключении переменных и постепенном переходе к эквивалентной системе уравнений с треугольной матрицей коэффициентов. Решение полученной системы не представляет проблем.

Исключение Гаусса рассмотрим на системе из трех уравнений

(3.7)

Выразим из первого уравнения системы значение переменной х₁ и подставим это выражение во второе и третье уравнения системы:

В результате второе и третье уравнения уже не содержат х₁:

что можно представить в виде

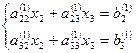
Аналогично выразим х₂ из второго уравнения и подставим это выражение в третье уравнение системы:

Окончательно система (3.7) преобразуется к виду :

Таким образом, за n-1 шагов исходная система линейных уравнений преобразуется к системе уравнений с верхней треугольной матрицей. Это прямой ход исключения Гаусса. Решение преобразованной системы уравнений с верхней треугольной матрицей, называется обратным ходом решения системы по Гауссу.

.