Блок схема алгоритма триангуляции

Обычно, при триангуляции матриц результирующие матрицы сохраняются на месте исходной. При этом матрица W занимает верхний, а L (без диагональных единиц) - нижний треугольник. В этом случае блок-схема расчетного процесса, по существу, совпадает с прямым ходом решения СЛУ метода Гаусса (раздел 3.5.1):

1. Цикл по исключаемым переменным k =1,…,n-1.

2. Цикл по строкам i=2,…,n.

3. = r = .

4. Цикл по текущим переменным j=i+1,…,n.

5. .

6. Next j; Next i ; Next k

Пример: Методом триангуляции матрицы проводимостей выполнить расчет электрической сети постоянного тока (рис. 4.1). УУН имеют вид

.

Шаг 1.

В процессе преобразования матрицы из второй строки вычитается управляющая, умноженная на . Аналогично относительно третьей строки

; .

.

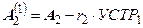
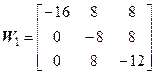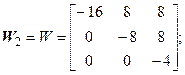
Алгоритм решения СЛУ методом Гаусса с триангуляцией матрицы может быть представлен в виде последовательности следующих макроопераций:

1. Разложение исходной матрицы A на треугольные сомножителиLи W.

2. Решение вспомогательной СЛУ с нижней треугольной матрицей L.

3. Решение СЛУ с верхней треугольной матрицей W.

Решение системы

Решение системы

4.2. Вычисление определителя

Триангуляция матрицы позволяет не только решить СЛУ, но и является основой наиболее эффективных методов нахождения определителя и обратной матрицы.

Известно, что определитель любой треугольной матрицы A равен произведению диагональных элементов. Это доказывается достаточно просто через последовательное разложение определителя по столбцам. Например,

.

Отсюда определитель нижней треугольной матрицы L равен единице, а верхней треугольной матрицы .

Известно, что определитель произведения матриц равен произведению определителей. В результате . Другое доказательство этого положения заключается в том, что преобразование строк матрицы А в алгоритме Гаусса не меняет определителя, следовательно, определители исходной матрицы А и верхней треугольной матрицы W, полученной в результате выполнения прямого хода совпадают.

Пример:

.

Алгоритм гауссовского исключения может быть рекомендован не только для расчетов на ЭВМ, но и ручных расчетов определителей матриц порядка 4 и выше.