
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Преобразования Гаусса с выбором главного элемента
В процессе матричных преобразований возможно появление ситуации, когда главный элемент управляющей строки равен нулю, akk =0, что делает недопустимым продолжение расчетов (управляющий столбец (аik/akk, i>k). Возникает ряд вопросов: СЛУ имеет решение? Если да, то какой должен быть алгоритм получения решения? Возможными путями решения указанной проблемы является: изменение очередности уравнений (замена строк); изменение очередности исключения переменных (замена столбцов); комбинация указанных процедур.
В процессе матричных преобразований Гаусса выполняется большое число арифметических операций, в каждой из которых возможно округление, т.е. вносится определенная погрешность, которая определяет погрешность решения. Дополнительным источником погрешности является сам принцип гауссовского исключения, где из строки i вычитается строка k, умноженная на коэффициент аik/akk, управляющего столбца. При относительно большом коэффициенте измененная строка практически может совпадать с ведущей строкой, что эквивалентно как бы отсутствию строки i. Это может привести к непредсказуемым результатам. Удельный вес, а следовательно, и информационная значимость строки i в конечном результате будут тем больше, чем меньше аik/akk. Отсюда процедура расчета должна быть такой, чтобы ведущий элемент akk. был как можно больше, а отношение аik/akk как можно меньше. В результате процедура исключения переменных получила свое дальнейшее развитие – гауссовское исключение с выбором главного элемента по строке, по столбцу или по блоку. Здесь важно запоминать очередность переменных и уравнений (столбец правой части).
Выбор главного элемента «по столбцу»
На очередном шаге k в столбце k начиная со строки k и ниже выбирается максимальный по модулю элемент. Пусть это будет элемент aik¹0. Строки i и k меняются местами. Если окажется, что все элементы столбца k равны нулю, то det A = 0. В этом случае матрица А является вырожденной или особенной. Решение СЛУ с такими матрицами рассматривается ниже.
Выбор главного элемента “по строке”
На очередном шаге k в строке k начиная со столбца k справа выбирается максимальный по модулю элемент. Пусть это будет элемент akj¹0. Столбцы меняются местами. Это эквивалентно замене нумерации переменных хj и хk. Если окажется, что все элементы строки k равны нулю, то det A = 0 и матрица А является вырожденной.
Выбор главного элемента «по блоку»
На очередном шаге k в блоке  выбирается максимальный по модулю элемент. Пусть это будет элемент ars¹0. Меняются местами как столбцы s, k, так и строки k, r. Если окажется, что максимальный элемент равен нулю, то det A = 0 и матрица А является вырожденной.
выбирается максимальный по модулю элемент. Пусть это будет элемент ars¹0. Меняются местами как столбцы s, k, так и строки k, r. Если окажется, что максимальный элемент равен нулю, то det A = 0 и матрица А является вырожденной.
Пример. Методом Гаусса с выбором главного элемента по строке, столбцу и по блоку решить систему линейных уравнений А 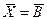
 .
.
Дата добавления: 2015-04-16; просмотров: 295; Мы поможем в написании вашей работы!; Нарушение авторских прав |