
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Учет слабой степени заполненности матрицы проводимостей
Описанный выше метод триангуляции для решения СЛУ учитывает две (постоянство и симметрию матрицы проводимостей) из трех особенностей решения задачи анализа установившихся режимов ЭЭС на базе системы УУН.
Третья и не менее важная из таких особенностей – слабая степень заполненности матрицы проводимостей отличными от нуля элементами. Матрицы проводимостей сетей достаточно большого объема (порядка тысячи узлов) примерно на 99% состоят из нулей. Для таких матриц стандартная процедура решения СЛУ весьма неэффективна, поскольку заключается в хранении и численной обработке нулей, требует неоправданно больших объемов оперативной памяти и времени ЭВМ.
Для решения задач, оперирующих со слабо заполненными матрицами, применяются специальные алгоритмические приемы решения СЛУ, например использование аппарата связных списков. При решении УУН, в частности, применяется так называемое оптимально упорядоченное исключение неизвестных по Гауссу (ОУГИ), позволяющие проводить операции преимущественно с ненулевыми элементами матрицы проводимостей и выбрать такой порядок исключения неизвестных, который обеспечивает минимально возможное появление новых ненулевых элементов в процессе преобразования матрицы. По существу ОУГИ своится к оптимальной нумерации узлов электрической схемы.
При выводе УУН было показано, чтокаждое уравнение i соответствует узлу i расчетной схемы и отражает его связи со смежными узлами. Исключение узла преобразует матрицу проводимостей, а, следовательно, и соответствующую ей топологию электрической сети.
Проанализируем основное расчетное соотношение метода Гаусса
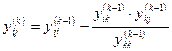 .
.
При исключении узла “k” между узлами i и j, связанными с k,появляется новая связь с проводимостью  . Если связь i – j ранее существовала, то выполняется коррекция (суммирование, поскольку
. Если связь i – j ранее существовала, то выполняется коррекция (суммирование, поскольку  ) проводимости по правилу электрического эквивалентирования параллельных связей.
) проводимости по правилу электрического эквивалентирования параллельных связей.
Данное соотношение представляет большой интерес, поскольку здесь ставится однозначное соотношение между математическим гауссовским исключением и электрическим преобразованием многолучевой звезды в многоугольник при эквивалентировании в пассивных электрических цепях. Во-первых, гауссовское исключение позволяет вспомнить формулу электрического эквивалентирования, а во-вторых, с помощью электрического эквивалентирования можно выполнять гауссовское исключение.
Число сторон многоугольника в зависимости от ранга (число смежных связей) исключаемого узла подчиняется соотношению  , в частности
, в частности
| r | |||||
| m |
Следовательно, число новых связей тем больше, чем выше ранг исключаемого узла. В то же время в процессе исключения узлов ранги оставшихся узлов уменьшаются. Отсюда основным направлением при нумерации узлов электрической сети должно быть возрастание номеров по мере увеличения рангов. Основная идея ОУГИ – минимум новых связей, а, следовательно, исключение узлов в порядке увеличения ранга.
Схема статического упорядочивания. Нумерация узлов здесь производится априори, перед исключением неизвестных в соответствии с рангом узлов. Начальные номера получают узлы с меньшим рангом. Если таких узлов несколько, то их порядок принимается произвольно. При расчете рангов узлов связи на базисный узел не учитываются, поскольку эти связи учитываются только в собственной проводимости и не влияют на число новых связей. Однако узлу, имеющему связи на базу, следует отдать наименьший среди всех узлов одинакового ранга приоритет, поскольку объем расчетов здесь выше.
Первая схема динамического упорядочивания. На каждом шаге исключается узел, имеющий минимальный (на данном шаге) ранг. Если узлов несколько, то выбирается любой. На следующем шаге ранги узлов пересчитываются для измененной электрической схемы сети. Замечания относительно связей на базу аналогичны схеме статического упорядочивания.
Вторая схема динамического упорядочивания. В отличие от предыдущей схемы выбирается такой узел, минимального ранга, удаление которого связано с появлением наименьшего числа новых ненулевых элементов.
Пример1: Исключение первого узла, ранга два, связанного со вторым и четвертым узлами, приводит появлению новой связи 2-4 с проводимостью y24=y12× y14 / (y14+ y12) (рис. 4.2).
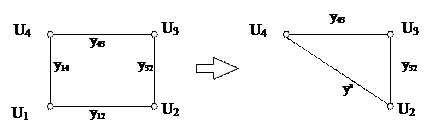
Рис. 4.2 Исключение узла, ранга два
В математической процедуре гауссовского исключения
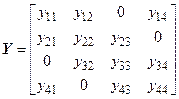

Новый элемент

Результирующая проводимость
 .
.
Это формула эквивалентной проводимости последовательного соединения двух элементов электрической сети.
Пример 2: Есть схема ЭС. Перенумеровать узлы в соответствии со схемой статического упорядочивания (рис. 4.3). Новые номера на схеме записаны в кружочках. В частности, первым узлом должен быть узел 9, ранга 1, претендентами на второй узел являются узлы ранга два: 1, 2, 4 (связь на базисный узел не учитывается, но этот узел имеет наименьший приоритет).
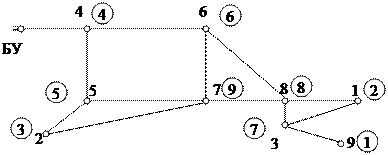

Рис. 4.3. Схема сети для нумерации узлов.
Дата добавления: 2015-04-16; просмотров: 330; Мы поможем в написании вашей работы!; Нарушение авторских прав |