Метод электрических преобразований

Выше было показано, что математические формулы преобразования матрицы проводимости при исключении переменной k эквивалентны формулам электрических преобразований при исключении узла k. Если учесть симметрию матрицы проводимостей и получаемых в процессе матричных преобразований блоков, то матрицы L,W, а также вектор 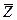можно получить в процессе электрических преобразований исходной электрической схемы.

При исключении узла k управляющая строка R_k формируется исходя из связей узла k в схеме после исключения предыдущих k-1 узлов. Управляющий столбец L_k определяется делением элементов строки R_k на диагональный элемент = / R_kk. При исключении узла k связанного с узлами i,j,m,…между всеми смежными узлами попарно появляются новые (дополнительные) связи с проводимостями . Результирующие проводимости связей получаются путем суммирования , где 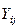- проводимость связи i-j на шаге k. При исключении узла его узловой ток разносится по смежным узлам пропорционально проводимостям . Это соответствует гауссовскому исключению для правой части СЛУ.

Значение , т.е. равно правой части УУН (току) для первого узла. На шаге k электрических преобразований определяется согласно выражению ,

т.е. является накопленным в процессе электрических преобразований током узла k с дополнительным током на базу.

Поскольку вектор формируется попутно, то матрица L для однократного расчета становится ненужной. Она необходима, если предполагается серия расчетов.

Пример. Выполнить расчет матриц L, W и вектора для схемы рис. 4.4. Расчеты сведены в табл. 4.1

Рис. 4.4. Пример расчетной схемы

Таблица 4.1

Y	Yб	LW	Yб	сум	Z	U
-1						-1							1,0	7,4
	-3					-1	-2						2,0	8,4
		-6				-0	-0	-6				-3	-23,0	10,1
			-5			-0	-0,5	-0,33	-3,83	2,167	-5/3		-15,7	9,4
				-5		-0	-0,5	-0,33	-0,57	-2,61	2,61	1,6	-24,5	9,4

Промежуточные расчеты. Первая строка триангулированной матрицы соответствует связям узла 1. Поскольку нет непосредственной связи с базисным узлом, то Z₁= =1. Исключение первого узла ранга 1 не приводит к появлению каких-либо новых связей. В части топологии сети производится простое исключение связи 1-2. Ток первого узла передается второму узлу. В результате =1+1=2.

В соответствии с измененной топологией сети записывается вторая строка триангулированной матрицы, отражающая связи с узлом 2. Следует обратить внимание, что собственная проводимость , а не -3, как это было для исходной схемы. Вторая компонента вектора z₂= =2.

В результате исключения узла 2 ранга два между узлами 4, 5 появляется дополнительная связь с проводимостью . Отсюда . Изменяются также собственные проводимости узлов 4, 5, но их определение на данном этапе не целесообразно, поскольку в процессе эквивалентных преобразований возможно изменение результирующей проводимости . Дополнительные токи в четвертый и пятый узлы = =2∙1/2=1. Эквивалентная схема на данном этапе имеет вид рис. 4.5.

Поскольку выполненные эквивалентные преобразования не коснулись третьего узла и смежных связей, то строка 3 результирующей матрицы W равна строке 3 исходной матрицы, а z₃ = = -3-20 = -23.

При исключении узла 3 появляются дополнительные связи . Отсюда новые значения проводимостей ; . Дополнительные токи = =-1. Следует еще раз отметить, что в эквивалентных преобразованиях участвуют исходные токи, а не правые части системы УУН . Результирующие токи =2-1=1.

После исключения третьего узла (читателю предлагается самостоятельно изобразить схему и проставить на ней величины проводимостей и токов) нулевые элементы четвертой строки матрицы W₄ равны (-3,83; 2,167). Компонента z₄= 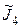=1-10∙5/3 = -15,7.

На последнем этапе исключается четвертый узел, как узел ранга 2. При этом ; ;Последняя строка W равна (0; 0; 0; 0; -2,61). компонента z₅= =1,6-10∙2,61 = -24,5.

Матрица L вычислена по описанному выше алгоритму (деление строки на диагональный элемент).

Решением СЛУ определяется искомый вектор напряжений =(7,4; 8,4; 10,1; 9,4; 9,4). В частности, U₅=-24,5/2,61=9,4, U₄= (-15,7-2,167∙9,4)/(-3,83)=9,4. Аналогично определяются остальные напряжения узлов.