
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение систем линейных уравнений методом простой итерации
Решение СЛУ 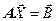 возможно не только прямыми, где предопределено число математических операций, но и итерационными методами. Для решения итерационным методом требуется получить рекуррентное соотношение
возможно не только прямыми, где предопределено число математических операций, но и итерационными методами. Для решения итерационным методом требуется получить рекуррентное соотношение  . С этой целью матрица коэффициентов представляется в виде А=S+T Тогда исходную СЛУ можно записать в виде:
. С этой целью матрица коэффициентов представляется в виде А=S+T Тогда исходную СЛУ можно записать в виде:
 или
или  .
.
Если матрица S-1 существует, то для определения решения СЛУ можно записать следующее рекуррентное выражение:

| (5.1) |
Итерационный метод определяется способом разбиения матрицы А на S и T. Для решения СЛУ в настоящее время применяются, в основном, методы простой итерации и Гаусса-Зейделя.
В методе простой итерации (метод Якоби) S –диагональная матрица из диагональных элементов матрицы А. ОтсюдаТ – матрица, диагональные элементы которой равны 0, а недиагональные совпадают с соответствующими элементами матрицы А.

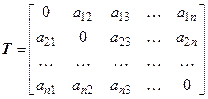
В каноническом виде рекуррентное выражение (5.1) метода простой итерации (метода Якоби) для УУН имеет вид

Пример: Рассмотрим систему УУН, соответствующую некоторой электрической сети с заданными узловыми токами (в качестве упражнения читателю предлагается изобразить схему этой сети)

Выразив из первого уравнения переменную U1, а из второго U2, получаем рекуррентное соотношение метода простой итерации:
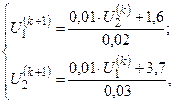
или  .
.
Для организации итерационного процесса предлагается брать в качестве начального приближения напряжения, равные напряжению балансирующего узла:  .
.
Итерация 1.

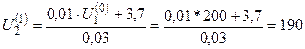 .
.
Итерация 2.
 ,
,
 .
.
Дальнейшие вычисления производятся аналогично. После 13 итераций получается почти точное решение:  .
.
Дата добавления: 2015-04-16; просмотров: 257; Мы поможем в написании вашей работы!; Нарушение авторских прав |