Алгоритм метода простой итерации

1. Ввод исходных данных . Начальные присвоения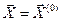

2. .

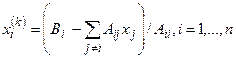3. .

4. Если 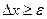, то перейти на п.2, иначе – на п.5

5. Печать результирующего вектора. Выход.

5.3. Ускоренный метод Зейделя-Гаусса

Ускоренный метод Зейделя-Гаусса отличается тем, что после вычисления нового, k+1 – го приближения по схеме новое значение переменной вычисляется по формуле:

,

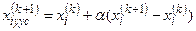что, при хорошем подборе α, приводит к ускорению расчетного процесса. Обычно значение a выбирают на интервале 0-2. Для решения УУН оптимальное значение a = 1,2…1,4. В зависимости от величины ускоряющего коэффициента a различают нижнюю релаксацию (a<1), верхнюю релаксацию (a>1), чистый метод Зейделя-Гаусса (a=1).

Пример: В рассмотренном примере использовать верхнюю релаксацию, a=1,25.

.

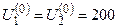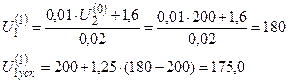
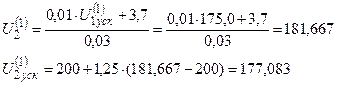
Дальнейшие итерации выполняются аналогично.

Дата добавления: 2015-04-16; просмотров: 7; Нарушение авторских прав