
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Доказательство на основе понятия расстояния от вектора до подпространства
Рассмотрим матрицу, построенную на векторах  =
=  ,
,  =
=  . Объем фигуры (параллелограмма), построенной на данных векторах определяется произведением модуля вектора
. Объем фигуры (параллелограмма), построенной на данных векторах определяется произведением модуля вектора  (объемфигуры векторного подпространства R1 меньшей размерности) на высоту h (минимальное расстояние от вектора
(объемфигуры векторного подпространства R1 меньшей размерности) на высоту h (минимальное расстояние от вектора 
 R1 до подпространства R1, образованного вектором
R1 до подпространства R1, образованного вектором  .
.
В подпространстве R1 найдется такой вектор 
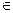 R1, которому соответствует разность
R1, которому соответствует разность  -
-  , модуль которой определяет высоту h. В свою очередь, вектор
, модуль которой определяет высоту h. В свою очередь, вектор  является, во-первых частью
является, во-первых частью  ,
,  =λ
=λ  , а, во-вторых,проекцией
, а, во-вторых,проекцией  на
на 
Исходя из определения скалярного произведения можно записать
 .
.
Отсюда
 = = 
| (7.4) |
В последнем выражении второй сомножитель является единичным вектором, направленным вдоль вектора  , и служит для преобразования скалярной величины (проекция) в векторную. Так как
, и служит для преобразования скалярной величины (проекция) в векторную. Так как  =λ
=λ  , то
, то
 , ,
| (7.5) |
а квадрат расстояния от  до подпространства, образованного вектором
до подпространства, образованного вектором 
 . .
| (7.6) |
При этом квадрат объема параллелепипеда
 . .
| (7.7) |
Подставляя координаты векторов, получаем
 .
.
что и требовалось доказать. Доказательство идентичности детерминанта матрицы и объема параллелепипеда на пространстве большей размерности выполняется по индукции, но в силу громоздкости доказательства оно здесь не приводится.
Оптимальное значение коэффициента λ (7.5), соответствующее вектору  можно получить, решая оптимизационную задачу.
можно получить, решая оптимизационную задачу.
Минимальное расстояние от вектора  до подпространства R1 определяется параметром λ из условия h=|
до подпространства R1 определяется параметром λ из условия h=|  -λ
-λ  ,|,
,|, 
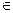 R1
R1  . Поскольку модуль числа всегда положителен, то это эквивалентно
. Поскольку модуль числа всегда положителен, то это эквивалентно  . Дифференцируя данное выражение по λ и приравнивая результат к нулю, получаем
. Дифференцируя данное выражение по λ и приравнивая результат к нулю, получаем
 , что совпадает с (7.5).
, что совпадает с (7.5).
Доказательство(7.7)на основе формулы площади параллелограмма
Высота h в параллелограмме определяется выражением  . При этом
. При этом
 .
.
Отсюда  , что совпадает с (7.7).
, что совпадает с (7.7).
Дата добавления: 2015-04-16; просмотров: 262; Мы поможем в написании вашей работы!; Нарушение авторских прав |