
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Норма матрицы
Первое (максимальное) собственное число  характеризует максимальное растяжение (при
характеризует максимальное растяжение (при  >1) или минимальное сжатие (при
>1) или минимальное сжатие (при  <1) вектора. Поскольку вычисления собственных чисел для матрицы большой размерности представляют значительные трудности, на практике часто используют оценку
<1) вектора. Поскольку вычисления собственных чисел для матрицы большой размерности представляют значительные трудности, на практике часто используют оценку  числовой характеристикой матрицы, называемой нормой матрицы
числовой характеристикой матрицы, называемой нормой матрицы  ,
, 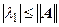 .
.
Норма матрицы является одной из характеристик матрицы. Поскольку матрица является отражением некоторого линейного преобразования, то неудивительно, что норма матрицы теоретически определяется через линейное преобразование верхней границей изменения длины вектора (представленный ниже оператор sup обозначает точную верхнюю границу)
 ,
,
т.е. норма матрицы характеризуется максимальным по модулю образом единичного вектора. Отсюда понятно соотношение 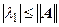 .
.
Используются три способа вычисления нормы матрицы.
1. Кубическая норма (норма по строкам) равна максимальной сумме модулей элементов строк 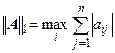 ,.
,.
2. Октаэдрическая норма (норма по столбцам) равна максимальной сумме модулей элементов столбцов,  .
.
3. Сферическая норма (Евклидова норма). 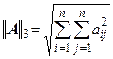 .
.
Свойства норм матрицы:
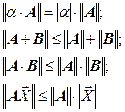
Для любой симметричной матрицы 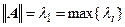 .
.
Дата добавления: 2015-04-16; просмотров: 618; Мы поможем в написании вашей работы!; Нарушение авторских прав |