Обособленность матрицы и точность решения СЛУ

Одной из областей использования линейных преобразований пространства и аппарата собственных чисел и собственных векторов является анализ чувствительности решений СЛУ и сходимости итерационных процессов.

Рассмотрим СЛУ 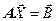. Вектор правой части СЛУ обычно представляет некоторую совокупность исходных или расчетных данных, которыми описываются реальные технические или физические величины, поэтому реально он обладает некоторой погрешностью . Отсюда и решение СЛУ также будет обладать погрешностью .

В этих условиях СЛУ следует рассматривать в виде

.

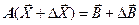Эту систему уравнений можно разделить на две:

Данные матричные уравнения отражают линейное преобразование с матрицей . При этом . В зависимости от направления и получается та или иная погрешность результирующего вектора .

Рассмотрим крайние случаи.

1. Вектор совпадает с первым собственным вектором (соответствующим 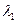), а с минимальным собственным вектором (соответствующим 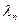), , . Отсюда относительная погрешность решения

,

где - так называемое число (Тодда) обусловленности матрицы. Таким образом, в рассматриваемом случае погрешность решения больше, нежели погрешность правой части СЛУ и тем больше, чем больше число обусловленности матрицы.

Число обусловленности матрицы характеризует:

· максимально возможную относительную погрешность решения СЛУ;

· чувствительность решения задачи к погрешности входных данных.

· степень вырожденности СЛУ (т.е. близость ее к линейно-зависимым). Чем ближе СЛУ к линейно-зависимым, тем больше число обусловленности r, если det (A)®0, то это значит , а ;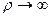

2. Вектор совпадает с , а D с 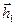, , . Отсюда относительная погрешность решения

.

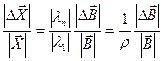Здесь погрешность исходных данных мало влияет на погрешность решения.

Обобщая рассмотренные крайние случаи, получаем

.

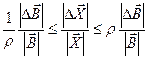Вычисление и весьма сложно. Поэтому часто используют оценку обусловленности с помощью норм: .

Если 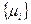- собственные числа обратной матрицы 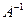. Тогда

; .