
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Оценка сходимости итерационного процесса решения СЛУ
Математический аппарат собственных чисел и векторов с успехом может быть использован при оценке сходимости итерационного процесса решения системы линейных уравнений 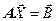 .
.
Итерационный метод определяется способом разбиения матрицы А на S и T, А =S+T . Как было упомянуто в разделе 5, в настоящее время при решении СЛУ применяются, в основном, методы простой итерации и Зейделя-Гаусса.
Для решения СЛУ методом простой итерации может быть используется рекуррентное соотношение (5.1) 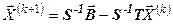 , где S- диагональная матрица, состоящая из диагональных элементов матрицы А, T=(A-S). Нетрудно показать, что
, где S- диагональная матрица, состоящая из диагональных элементов матрицы А, T=(A-S). Нетрудно показать, что 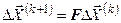 , где
, где 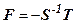 . В данном представлении
. В данном представлении 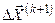 является образом вектора
является образом вектора 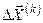 при линейном преобразовании с матрицей F. Отсюда для обеспечения сходимости итерационного процесса (
при линейном преобразовании с матрицей F. Отсюда для обеспечения сходимости итерационного процесса ( 
 ) необходимо, чтобы линейное преобразование было бы сжимающим,
) необходимо, чтобы линейное преобразование было бы сжимающим,  .
.
Для системы УУН в методе простой итерации

Поскольку  , причем возможно точное равенство (для узлов, не связанных с базой) то
, причем возможно точное равенство (для узлов, не связанных с базой) то 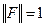 , т.е. нет абсолютной гарантии сходимости итерационного процесса.
, т.е. нет абсолютной гарантии сходимости итерационного процесса.
В методе Зейделя-Гаусса, как это было отмечено в 5.2, рекуррентное выражение имеет вид:  . При этом
. При этом
 ,
,  .
.
Здесь также нет гарантии сходимости итерационного процесса, поскольку 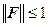 .
.
Дата добавления: 2015-04-16; просмотров: 254; Мы поможем в написании вашей работы!; Нарушение авторских прав |