
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дифференциальные уравнения и методы их решения
Общие положения
Режимы электроэнергетических систем, как правило, описываются динамическими процессами, где вектор  параметров (напряжения, токи, мощности) является функцией времени. При анализе таких процессов рассматривается взаимосвязь между
параметров (напряжения, токи, мощности) является функцией времени. При анализе таких процессов рассматривается взаимосвязь между  и его производными, в результате чего формируется система дифференциальных уравнений.
и его производными, в результате чего формируется система дифференциальных уравнений.
Дифференциальное уравнение (ДУ) - это уравнение, содержащее анализируемые функции, их производные различных порядков и независимые переменные.
Если производные, входящие в уравнение, берутся по одному переменному (например, время), то такие ДУ называются обыкновенными.
Если в уравнении встречаются производные по нескольким переменным, то такие уравнения называются дифференциальными уравнениями в частных производных. Далее будут рассматриваться обыкновенные дифференциальные уравнения.
Для физических процессов независимым параметром, по которому ведется дифференцирование, чаще всего, является время t. Обыкновенное ДУ представляется в виде
 .
.
Порядк ДУ определяется порядком наивысшей производной.
Решением ДУ называется всякая функция 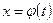 , при подстановке которой в уравнение, последнее превращается в тождество.
, при подстановке которой в уравнение, последнее превращается в тождество.
Можно выделить две основные задачи решения ДУ:
· определение значений 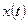 в некоторый период времени при заданных начальных условиях (задача Коши);
в некоторый период времени при заданных начальных условиях (задача Коши);
· качественный анализ поведения переменной 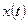 , т.е. получение суждения о свойствах процесса без определения самих решений. Эта задача называется задачей анализа устойчивости уравнений.
, т.е. получение суждения о свойствах процесса без определения самих решений. Эта задача называется задачей анализа устойчивости уравнений.
В соответствии с разными целями и видами уравнений применяются следующие методы (способы) решения ДУ:
аналитический метод позволяет получить аналитическую запись выражения 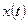 . Этот способ всегда предпочтителен, так как он позволяет определить точное выражение
. Этот способ всегда предпочтителен, так как он позволяет определить точное выражение 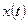 ;
;
качественные методы на основе заданных критериев позволяют судить о характере решения ДУ без получения точного решения;
численные методы - решение представляется в виде некоторого набора приближенных значений функции 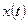 через заданные промежутки времени
через заданные промежутки времени 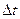 .
.
Численные методы позволяют получать решения любых ДУ и широко используются в практике.
Дата добавления: 2015-04-16; просмотров: 243; Мы поможем в написании вашей работы!; Нарушение авторских прав |