Преобразование подобия

Совокупность линейно-независимых собственных векторов образует базис. При этом матрица перехода из исходного базиса в новый представляется совокупностью координат собственных векторов в исходном базисе

.

Соотношения в матричном виде можно представить как

,

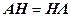(7.8)

где - диагональная матрица из собственных чисел: = .

Нельзя писать , так как , что не соответствует действительности, и, кроме того, при умножении матрицы H на справа действительно, каждый собственный вектор (столбец матрицы H) умножается на соответствующее собственное число

,

в то время как умножение на диагональную матрицу слева равносильно умножению на коэффициенты строк, а не столбцов, что противоречит математическому смыслу собственных векторов:

.

Умножив уравнение (7.8) сначала справа, а затем слева на матрицу , получим

; .

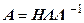(7.9)

МатрицыАи L представляют собой одно и то же линейное преобразование, записанное в различных системах координат. Матрица А показывает преобразование в координатах базиса , а матрица L показывает тоже преобразование в координатах базиса .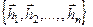

Итак, одному и тому же линейному преобразованию в разных базисах соответствует отличающиеся матрицы.

Базис1: – A, ,

Базис 2: 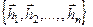- L ,

Базис 3: – , ,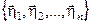

где B= , (см.п.7.2)

Матрицы А и L называются подобными, т.к. соответствуют одному и тому же преобразованию. Определители этих матриц равны. Отсюда определитель матрицы равен произведению всех его собственных чисел

.

Структурная диаграмма преобразования векторов представлена на рис. 7.9. В частности, если требуется преобразовать вектор из базиса в базис , то необходимо умножить его на матрицу H^-1.

С помощью данной диаграммы легко получается соотношение подобия (7.9), которое показывает переход от вектора к его образу 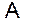по и против часовой стрелки.