Проверка шин на электродинамическую и термическую устойчивость.

Сборные шины выбирают по допустимому нагреву из условия ,

где I_расч – расчетный ток, I_доп – длительно допустимый ток по условию нагрева.

Выбранные сечения шин должны быть проверены на термическую и электродинамическую стойкость.

При прохождении токов КЗ в шинах и других токоведущих частях возникают электродинамические усилия, которые создают изгибающие моменты и напряжения в металле. Критериями электродинамической стойкости или механической прочности шин являются максимальные напряжения, которые не должны превышать допустимых для данного материала значений.

σ_р ≤ σ_доп, где σ_р, σ_доп – соответственно расчетное и допустимое напряжения материала на изгиб.

Шину, закрепленную на изоляторах, можно рассматривать как многопролетную балку. Наибольшее напряжение в металле при изгибе

где М – максимальный изгибающий момент, Н·м; W – момент сопротивления шины, м³.

При расположении шин на ребро , при расположении плашмя .

Здесь b и h – соответственно ширина (узкая сторона) и высота (большая сторона) сечения шины, м.

Выражение для изгибающего момента М, создаваемого ударным током КЗ, можно получить, если рассматривать шину как равномерно нагруженную многопролетную балку.

где l – расстояние между изоляторами, м; ζ – коэффициент, равный 10 для крайних пролетов и 12 для остальных пролетов; F – сила взаимодействия между проводниками при протекании по ним ударного тока КЗ.

Для трехфазных шин в качестве расчетного принимают ударный ток трехфазного КЗ. Причем расчет электродинамической стойкости проводится для проводников средней фазы, поскольку на них действуют наибольшие значения ЭДУ.

. Здесь а – расстояние между шинами, l – расстояние между изоляторами фазы, К_ф – коэффициент формы, определяемый по кривым Двайта (обычно К_ф ≈ 1).

Механические напряжения проводниковых материалов не должны превышать 140 МПа для меди (марки МТ) и 70 МПа для алюминия (марки AT).

При расчете разрушающего усилия на изолятор 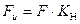, где К_н = 1 при расположении шин плашмя, К_н = (h_из + b + 0,5h)/ h_из при расположении шин на ребро. Для открытых распределительных устройств, где изоляция электрических аппаратов подвергается действию ветра, гололеда, натяжения проводников, при расчете вводят коэффициент запаса К_з = 3 (нагрузка на изоляторы должна быть в 3 раза меньше предельной разрушающей). Для закрытых РУ коэффициент запаса снижается до 1,5-1,7.

Шины, как и любая другая система, совершают свободные или собственные колебания в виде стоячих волн. Если частота вынужденных колебаний под действием ЭДУ будет близка к частоте собственных колебаний, то может наступить механический резонанс и разрушение аппарата даже при сравнительно небольших усилиях. Поэтому при расчете электродинамической стойкости необходимо учитывать возможность появления механического резонанса.

Частоту собственных колебаний шин, расположенных в одной плоскости, можно определить по выражению.

, где 1 – пролет шины, м; Е – модуль упругости материала шины, Па; J – момент инерции поперечного сечения шины, м⁴; m – масса одного погонного метра шины, кг/м. Момент инерции J определяется относительно оси сечения, перпендикулярной плоскости колебаний. При расположении шин на ребро , при расположении плашмя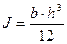

При частоте собственных колебаний более 200 Гц явление резонанса не учитывают. Если же частота f₀ < 200 Гц, то для исключения возникновения резонанса изменяют расстояние между опорными изоляторами.

Для соблюдения условий термической стойкости шин необходимо, чтобы проходящий по ним ток КЗ не вызывал повышение температуры свыше предельно допустимой. Минимальное термически устойчивое сечение шины или проводника должно отвечать условию: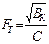

где В_к – расчетный тепловой импульс тока. С – термический коэффициент (функция), зависит от материала шин. Для практических расчетов В_к = I_¥² t_пр,

где I_¥ – действующее значение установившегося тока КЗ; t_пр – приведенное время действия тока КЗ.

Под приведенным временем понимаются время, в течении которого установившийся ток КЗ I_¥ выделяет то же количество теплоты, что и изменяющийся во времени ток КЗ за действительное время t.

t_пр=t_пр.п + t_пр.а, где t_пр.п, t_пр.а – периодическая и апериодическая составляющие приведенного времени КЗ. Периодическую составляющую времени t_пр.п определяют по кривым зависимости t_пр.п = f(β''). Здесь β'' = I''/I_¥, где I'' – действующее значение периодической составляющей тока КЗ в начальный период (начальный сверхпереходный ток КЗ). Если ЭДС источника неизменна, что имеет место при питании от сети неограниченной мощности, то считают, что I'' = I_¥ и β'' = 1.

Приведенное время периодической составляющей t_пр.а = 0,005β''². Термический коэффициент С аналитически можно определить из выражения С = ,

где А_ΘКОН, А_ΘНАЧ – тепловые функции или значения среднеквадратичных импульсов тока, соответствующих конечной и начальной температуре шины или проводников при КЗ, А²с/мм⁴.

Обычно в справочниках приводятся кривые зависимости температуры от значений расчетного интеграла А_Θ для различных материалов. Расчет шин на термическую стойкость с помощью этих кривых производят следующим образом. Задается допустимая температура проводника при КЗ и при номинальном токе, затем по кривым находят соответствующие значения А_ΘКОН, А_ΘНАЧ. Для алюминиевых шин при номинальных условиях приняты температура начальная 70^о С, конечная – допустимая – 200^о С. В этом случае, термический коэффициент С = 95.

Таким образом, для алюминиевых шин минимальное термически стойкое сечение аналитически можно найти из выражения: .

При графоаналитическом методе расчета необходимо, чтобы θ_кр ≤ θ_доп, где θ_кр – температура нагрева шины током КЗ; θ_доп – допустимая температура нагрева, зависящая от материала шин.

Температуру нагрева шины током КЗ определяют по кривым в зависимости от начальной температуры, материала шины и теплового импульса.