Идеальные газы и основные газовые законы.

Под идеальным газом понимают воображаемый газ, в котором отсутствуют силы притяжения между молекулами, а собственный объем молекул очень мал по сравнению с объемом межмолекулярного пространства. В действительно существующих газах при высоких температурах и малых давлениях можно пренебречь силами притяжения между молекулами и объемом самих молекул. Поэтому такие газы можно считать идеальными.

В тех газах, которые находятся в состояниях, достаточно близких к сжижению, нельзя пренебречь силами притяжения между молекулами и объемом последних. Такие газы нельзя отнести к идеальным, и их называют реальными газами.

Основное уравнение кинетической теории газов имеет вид:

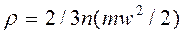,(2.1)

где 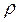- давление идеального газа;

n- число молекул в 1 м³ газа (концентрация молекул);

m- масса одной молекулы;

w- средняя квадратичная скорость поступательного движения молекул;

- средняя кинетическая энергия поступательного движения одной молекулы.

Таким образом, основное уравнение кинетической теории газов устанавливает связь между давлением газа, средней кинетической энергией поступательного движения молекул и их концентрацией. Основные зависимости, характеризующие соотношение между параметрами идеального газа при некоторых вполне определенных условиях изменения его состояния, легко получаются из основного уравнения кинетической теории газов. До этого они были получены экспериментальным путем.

Так, если температура газа не изменяется (T=const), то давление газа и его объем связаны следующей зависимостью (закон Бойля-Мариотта);

(2.2)

Если давление газа остается постоянным (P=const), то соотношение между удельным объемом газа и его абсолютной температурой подчиняется закону Гей-Люссака;

(2.3)

или

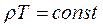(2.4)

Для газов, взятых при одинаковых температурах и давлениях, имеет место следующая зависимость, полученная на основе закона Авогадро:

, (2.5)

где μ - молекулярная масса газа;

ρ - плотность вещества.

Так как ρ=1/ν

(2.6)

Величина μν представляет собой объем килограмм-молекулы или киломоля (кмоль) газа.

Принято относить 1м³ газа к нормальным условиям, при которых рабочее вещество находится под давлением:

Р= 101325 Па и Т= 273,15 К (760 мм рт.ст. и 0°С).

Объем 1 кмоля всех идеальных газов равен 22,4136 м³/кмоль при нормальных условиях.

Плотность газа при нормальных условиях определяется из равенства:

(2.7)

Пользуясь этой формулой, можно найти удельный объем любого газа при нормальных условиях:

(2.8)

Характеристическое уравнение идеального газа или уравнение состояния связывает между собой основные параметры состояния – давление, объем и температуру – и может быть представлено следующими уравнениями:

(2.9)

(2.10)

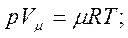(2.11)

где Р – абсолютное давление газа в Па;

V- объем газа в м³:

M- масса газа в кг;

v- удельный объем газа в м³/кг;

- объем одного кмоля газа в м³/кмоль;

R- газовая постоянная для 1 кг газа в Дж/(кг·К);

Т- абсолютная температура, К:

- универсальная газовая постоянная 1 кмоля газа в Дж/(кмоль·К).

Каждое из этих уравнений отличается от другого лишь тем, что относится к различным массам газа: первое – к М кг; второе - к 1 кг, третье – к 1 кмолю газа.

Численное значение универсальной газовой постоянной легко получить из уравнения (2.11) при подстановке значений входящих в него величин при нормальных условиях:

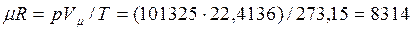
Газовую постоянную, отнесенную к 1 кг газа, определяют из уравнения

(2.12)

Где μ - масса 1 кмоля газа в кг (численно равная молекулярной массе газа).

Пользуясь характеристическим уравнением для двух различных состояний какого-либо газа, можно получить выражение для определения любого параметра при переходе от одного состояния к другому, если значения остальных параметров известны:

(2.13)

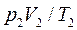(2.14)

Если объем газа известен, уравнение (2.14) представляют в виде:

(2.15)

В правой части уравнения все величины взяты при нормальных условиях, а в левой – при произвольных значениях давления и температуры.

Уравнение можно переписать следующим образом:

Следовательно,

(2.16)

Данное уравнение позволяет найти плотность газа при любых условиях, если значение его для определенных условий известно.

Задачи

2.1. Какой объем занимает 1 кг азота при температуре 70 ⁰С

и давлении 0.2 МПа? Ответ: V=0.5 м³.

2.2. Плотность воздуха при нормальных условиях r_н=1.293 кг/м³.

Чему равна плотность воздуха при давлении Р=1.5 МПа и температуре t=20 ⁰С.

Ответ: r=17.82 кг/м³.

2.3. Во сколько раз объем определенной массы газа при температуре t= -20 ⁰С меньше, чем при t=+20 ⁰С, если давление в обоих случаях одинаковое?

При постоянном давлении объем газа изменяется по уравнению(2.3):

V/T=const или V2/V1=T2/T1,

следовательно,

V₂/V₁=(273+20)/(273-20)=1.16.

Ответ: в 1.16 раза.

2.4. В воздухоподогреватель парового котла подается вентилятором 130 000 м³/ч воздуха при температуре 30 ⁰С.

Определить объемный расход воздуха на выходе из воздухоподогревателя, если он нагревается до 400 ⁰С при постоянном давлении.

Ответ: V=288 700 м³/ч.

2.5. Найти массу 5 м³ водорода ,5 м³ кислорода и 5 м³ углекислоты при давлении 0.6 МПа и температуре 100 ⁰С.

Решение:

Воспользуемся уравнением идеального газа для произвольного количества газа

РV=МRT.

Следовательно,

M=РV/RT=0.6·10⁶·5/R·373=8042.8/R.

Значения газовых постоянных берем из табл.IV(см. приложения):

R_H2=4124 Дж/(кг К); R_O2=259.8 Дж/(кг К);

R_CO2=188.9 Дж/(кг К).

Тогда

M_H2=8042.8/24124=1.95 кг;

M_O2=8042.8/259.8=30.9 кг;

M_CO2=8042.8/188.9=42.6 кг.

Ответ: M_H2=1.95 кг; M_O2= 30.9 кг; M_CO2 =42.6 кг.

2.6. В цилиндре диаметром 0.6 м содержится 0.41 м³ воздуха при Р=0.25 МПа и t₁=35 ⁰С.

До какой температуры должен нагреваться воздух при постоянном давлении, чтобы движущийся без трения поршень поднялся на 0.4 м?

Ответ: t₂=117.6 ⁰С.

2.9. В цилиндрическом сосуде, имеющем d=0.6 м и высоту h=2.4 м, находится воздух при температуре 18 ⁰С. Давление воздуха составляет 0.765 МПа. Барометрическое давление (приведенное к нулю) равно 101858 Па. Определить массу воздуха в сосуде.

Ответ: М=7.04 кг.

2.10. Баллон с кислородом емкостью 20 л находится под давлением 10 МПа при 15 ⁰С. После израсходования части кислорода давление понизилось до 7.6 МПа , а температура упала до 10 ⁰С.

Определить массу израсходованного кислорода.

Решение:

Из уравнения состояния идеального газа

M=РV/RT.

Следовательно, до расходования кислорода масса его составляла

М₁=10·10⁶·0.02/259.8·288=2.673 кг,

а после израсходования

М₂=7.6·10⁶·0.02/259.8·283=2.067 кг,

таким образом , расход кислорода

2.673-2.067=0.606 кг.

Ответ: М₁-М₂=0.606 кг

2.11. Резервуар объемом 4 м³ заполнен углекислым газом . Найти массу и силу тяжести (вес ) газа в резервуаре, если избыточное давление газа Р_ман =40 кПа, температура его t=80 ⁰С, а барометрическое давление воздуха В=102.4 кПа.

Ответ: М=8.64 кг; G=84.8 H.

2.12.Сосуд емкостью V=10 м³ заполнен 25 кг углекислоты. Определить абсолютное давление в сосуде, если температура в нем t=27 ⁰C.

Решение:

Из уравнения состояния идеального газа имеем

Р_абс =MRT/V=25·8314·300/44·10=141 700 Па=141.7 кПа.

Ответ: Р_абс =141.7 кПа

2.13. Баллон емкостью 0.9 м³ заполнен воздухом при температуре 17 ⁰С, присоединенный к нему вакууметр показывает разрежение Р_вак=80 кПа. Определить массу воздуха в баллоне, если показание барометра равно 98.7 кПа.

Ответ: М=0.2018 кг.

2.14. Определить подъемную силу воздушного шара, наполненного водородом, если объем его на поверхности земли равен 1 м³ при давлении р=100 кПа и температуре t=15 ⁰C.

Решение:

На поверхности земли подъемная сила воздушного шара, наполненного водородом, равна разности сил тяжести (весов) воздуха и водорода в объеме шара:

G=G_возд-G_H2=(M_воздg-М_H2) g=gV(r_возд-r_Н2),

где g=9.81 м/с²-ускорение свободного падения.

Значения плотностей воздуха и водорода могут быть определены из уравнения состояния

Рv=RT, откуда 1/v=r=Р/RT.

Значения газовых постоянных могут быть легко вычислены или взяты из табл. IV (см. приложения); R_возд=287 Дж/(кг К); R_H2=4124 Дж/(кг К).

Так как давление водорода и воздуха равно 0.1 МПа, то

r _возд=0.1·10⁶/287·288=1.210 кг/м³;

r _H2=0.1·10⁶/4124·288=0.084 кг/м³.

Следовательно, подъемная сила шара

DG=gV(r_возд-r_Н2)=9.81·1· (1.210-0.084)=11.1 Н.

2.15. Газохранилище объемом V=100 м³ (Рис 2.1) наполнено газом коксовых печей.

Рис. 2.1

Определить массу газа в газохранилище, если t=20⁰С, В=100 кПа, а показание манометра, установленного на газохранилище р=133.3 кПа. Газовую постоянную коксового газа принять равной 721 Дж/(кг К).

Ответ: М=47.6 кг.

2.16. Воздух, заключенный в баллон емкостью 0.9 м³, выпускают в атмосферу. Температура его вначале равна 27 ⁰С. Найти массу выпущенного воздуха, если начальное давление в баллоне составляло 9.32 МПа, после выпуска -4.22 МПа, а температура воздуха снизилась до 17 ⁰С.

Ответ: 51.8 кг.

2.17. Дутьевой вентилятор подает в топку парового котла 102000 м³/ч воздуха при температуре 300 ⁰С и давлении 20.7 кПа. Барометрическое давление воздуха в помещении В=100.7 кПа.

Определить часовую производительность вентилятора в м³ (при нормальных условиях).

Ответ: Q=48 940 м³/ч.