Циклы холодильных установок

Холодильные установки служат для искусственного охлаждения тел ниже температуры окружающей среды. Рабочее тело в холодильных машинах совершает обратный круговой процесс, в котором в противоположность прямому циклу затрачивается работа извне и отнимается теплота от охлаждаемого тела.

Идеальным циклом холодильных машин является обратный цикл Карно. В результате осуществления этого цикла затрачивается работа 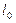, тепло от холодного тела переносится к более нагретому телу.

Отношение отведенной от охлаждаемого тела теплоты (произведенного холода) к затраченной работе 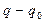носит название холодильного коэффициента и является характеристикой экономичности холодильной машины:

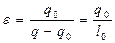(12.1)

Очевидно, максимальное значение холодильного коэффициента при заданном температурном интервале равно холодильному коэффициенту обратного цикла Карно, т.е.

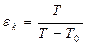(12.2)

Отношение характеризует степень термодинамического совершенства применяемого цикла.

В качестве холодильных агентов применяют воздух и жидкости с низкими температурами кипения: аммиак, углекислоту, сернистый ангидрид и в последнее время – фреоны.

Цикл воздушной холодильной установки

Холодопроизводительность 1 кг воздуха 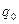определяется из уравнения

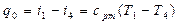, (12.3)

где - температура воздуха, выходящего из холодильной камеры и поступающего в компрессор;

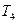- температура воздуха, входящего в холодильную камеру;

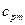- средняя массовая теплоемкость воздуха при постоянном давлении.

Работа, затраченная компрессором

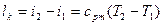, (12.4)

где 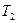- температура воздуха после его сжатия в компрессоре.

Работа, полученная в расширительном цилиндре

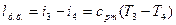, (12.5)

где 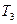- температура воздуха перед расширительным цилиндром.

Работа, затраченная в цикле, определяется по уравнению:

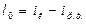(12.6)

Расход холодильного агента равен

, (12.7)

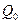где и 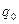- соответственно холодопроизводительность установки и холодопроизводительность 1 кг воздуха в кДж/с и кДж/кг (или в ккал/с и ккал/кг).

Холодильный эффект

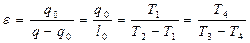(12.8)

Холодильный коэффициент можно выразить также в функции отношения конечного и начального давлений в компрессоре:

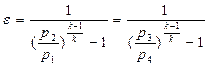(12.9)

Теоретическая мощность, необходимая для привода компрессора

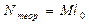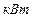, (12.10)

если 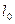выражено в кДж/кг.

Затрата работы в компрессоре при адиабатном сжатии определяется по формуле:

(12.11)

Холодопроизводительность 1 кг холодильного агента

, (12.12)

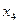где - теплота парообразования, а и - соответственно степень сухости пара после испарения и после редукционного вентиля.

Тепловая нагрузка конденсатора определяется по формуле

(12.13)

Задачи

12.1. На рис. 12.1 представлена схема, а на рис. 12.2 изображен цикл паровой компрессорной холодильной установки. Пар аммиака при температуре t₁ = -10°С поступает в компрессор В, где адиабатно сжимается до давления, при котором его температура t₂= 20° С,а сухость пара х₂ = 1. Из компрессора аммиак поступает в конденсатор С, где при постоянном давлении обращается в жидкость (xз = О), после чего в особом расширительном цилиндре D адиабатно расширяется до температуры t₄ = -10°С; при этой же температуре аммиак поступает d в охлаждаемое помещение А, где, забирая теплоту от охлаждаемых тел, он испаряется, образуя влажный пар со степенью сухости x₁.

Определить холодопроизводительность аммиака, тепловую нагрузку конденсатора, работу, затраченную в цикле, и холодильный коэффициент.

рис. 12.1

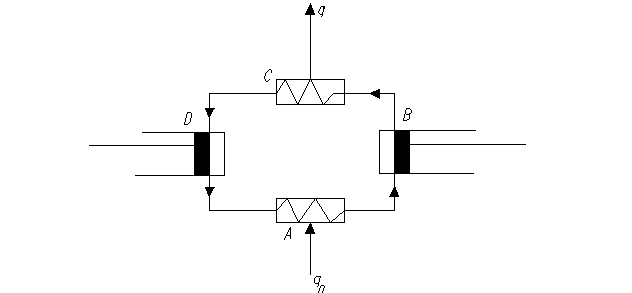
рис. 12.2

Решение:

Холодопроизводительность аммиака, т. е. количество теплоты, поглощаемой 1 кг аммиака в охлаждаемом помещении, по уравнению (12.12)

q₀ =i₁ -i₄ = r (x₁ - x₄), при t₁=-10 °C r₁ = 1296.6 кДж/кг [10].

Значения x1 и x4 определяем или при помощи диаграммы T-S, или аналитически. В последнем случае используем постоянство энтропии

в обратимом адиабатном процессе. Следовательно, в процессе 1-2

s₂ = s_l = s'_l + (s'l + sl) x_1.

s_l = 4,0164 кДж/(кг. К); Si = 8,9438 кДж/(кг. К);

s₂ = 8.5658 кДж/(кг. К). Тогда x₁=

=(s”₂-s₁)/(s”₁-s₁’)’=(8.5658-4.0164)/(8.9338-4.0164)=0.925.

Точно таким же образом определяем x₄

x₄=(s’₃-s’₁)/(s”₁-s’₁)=(4.5155-0.1015)/4.9174=0.1015.

Следовательно, q =1296,6 (0,925-0.1015) = 1067,8 кДж/кг,

Тепловая нагрузка конденсатора, т. е. количество теплоты, отводимой с охлаждающей водой, по уравнению 9 = i₂-i₃=r₂.

По табл. [10] при t=20°C r₂=1186.9 кДж/кг, следовательно,

q = 1186,9 кДж/кг.

Работа, затраченная в цикле,

Lо=q-q₀= 1186,9- 1067,8 = 119,1 кДж/кг. Xолодильный коэффициент

e=q₀/L₀=1067.8/119.1=8.96.

12.2. В схеме аммиачной холодильной установки, приведенной в предыдущей задаче, расширительный цилиндр заменяется редукционным вентилем. Новая схема предст­авлена на рис. 12.3.

Рис. 12.3

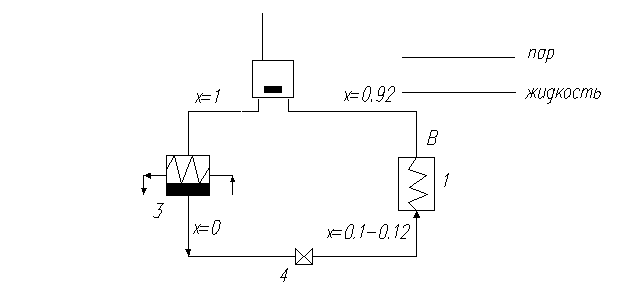
В остальном все условия предыдущей задачи сохраняются.

Определить новое значение холодильного коэффициента e и сравнить его с e“ для схемы с расширительным цилиндром.

Ответ: e = 8,17; e/e“= 0,927.

12.3. Компрессор аммиачной холодильной установки всасывает пар аммиака при температуре t₁. = -10° С и степени сухости x₁= 0,92 и сжимает его адиабатно до давления, при котором его температура t₂ = 20° С и степень сухости х₂= 1. Из компрессора пар аммиака поступает в конденсатор, в котором охлаждающая вода имеет на входе температуру t_в= 12°С, а на выходе t”_в=20°.

В редукционном (регулирующем) вентиле жидкий аммиак подвергается дросселированию до 0,3 МПа, после чего направляется в испаритель, из которого выходит со степенью сухости х = 0.92 и снова поступает в компрессор. Теплота, необходимая для испарения аммиака, заимствуется из рассола, имеющего на входе в испаритель, температуру t'_p =-2°С, а на выходе из него температуру t”_p =-5° С.

Определить теоретическую мощность двигателя холодильной машины и часовой расход аммиака, рассола и .охлаждающей воды, если холодопроизводительность установки Q₀= 58.15 кДж/с. Теплоемкость рассола принять, равной 4,19 кДж/(кг К).

Решение:

Условный цикл аммиачной холодильной установки для данных, указанных в задаче, показан на рис. 12.3.

Работа, затраченная на компрессор, определяется по уравнению L_k=i₂-i₁.

Энтальпия пара, выходящего из компрессора, поскольку он является сухим, насыщенным, определяется по таблицам насыщенного пара аммиака[10]:

i₂= i” = 1699,4 кДж/кг; r₂= 1186,9 кДж/кг.

Энтальпия влажного пара, всасываемого компрессором, определяется по формуле для влажного паpa i₁ =i_x = i”₁ + r₁x.

По табл. [10] находим

i’1=372,6 кДж/кг; r1=1296,6 кДж/кг; откуда i1 =

= 372,6 + 1296.6∙0.92 = 1505,5 кДж/кг.

таким образом, paботa, затраченная на привод компрессора,

L_k=i₂-i₁ =1699,4-1565,6 =133,8 кДж/кг.

Для определения мощности двигателя холодильной машины необходимо знать количество холодильного агента (аммиака), всасываемого компрессором. Оно определяется из уравнения (12.7):

М_а=Q₀/q₀.

Холодопроизводительность Qo аммиачной машины известна, а величина q₀ определяется по формуле (12.12)

q₀ =i₁ - i₄

Так как процесс дросселирования (линия 3-4)характеризуется равенством начального и конечного значений энтальпии, то

i₄= i₃= i’₂ = 512,5 кДж/с.

Следовательно, q₀ = 1565,5- 512,5 == 1053 кДж/кг.

Количество холодильного агента (аммиака) М_a =58.15/1053= 0,0552 г/c.

Таким образом, теоретическая мощность двигателя формуле (12.10)

N_теор=М∙L₀= 0.0552.133,8 = 7.39 кДж/с = 7,39 кВт. Потребное количество рассола по уравнению: Мр = с (t'p - t"р) при с= 4,19 кДж/(кг.К)

Мр=58.15/(4.19∙(-2-(-5)))= 4,626 кг/с.

Необходимее количество охлаждающей воды определяем из уравнения

Мв=Маr/c(t”в-t’в)=0.0552∙1186.9/4.19∙ (20-12)=1.96 кг/с.