Изобарный процесс

Процесс сообщения или отнятия теплоты при постоянном давлении называется изобарным (P=const)

Зависимость между начальными и конечными параметрами процесса

(8.1)

Работа 1 кг газа

(8.2)

или

. (8.3)

Для М кг газа

(8.4)

или

. (8.5)

Если в процессе 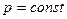участвует М кг или V_н м³ газа, то количество теплоты

(8.6)

Задачи

8.1. Какое количество теплоты необходимо затратить , чтобы нагреть 2 м³ воздуха при постоянном избыточном давлении р=0.2 МПа от t₁=100°С до t₂=500°С? Какую работу при этом совершит воздух?

Давление атмосферы принять равным 101 325 Па.

Решение:

Согласно уравнению

q_p=c_pm2t₂-c_pm1t₁.

c_pm1=1.0061 кДж/кг К; c_pm2=1.0387 кДж/кг К.

Следовательно,

q_p=1.0387∙500-1.0061∙100=418.7 кДж/кг.

Массу воздуха определяем из характеристического уравнения

M=РV/RT=(0.2+0.1013)10⁶∙2/287∙373=5.63 кг.

Таким образом ,

Q_p=Mq_p=5.63∙418.7=2357 кДж.

Количество теплоты можно получить не только по массе воздуха , но и по его объему. В этом случае уравнение следует написать так:

q_p=с’_pm2t₂-c’_pm1t₁.

Пользуясь табл. 4.2, получаем

c’_pm1=(c’_pm)₀¹⁰⁰=1.3004 кДж/м³ К;

c’_pm2=(c’_pm)₀⁵⁰⁰=1.3427 кДж/м³ К.

Тогда

q_p=1.3427∙500-1.3004∙100=541.4 кДж/м³.

Объем воздуха должен быть приведен к нормальным условиям. Согласно уравнению

V_н=pVT_н/Tp_н=0.3013∙2∙273/373∙0.1013=4.35 м².

Таким образом,

Q_p=q_pV_н=541.4∙4.35=2356 кДж.

Работа газа по уравнению

L=MR(t₂-t₁)=5.63∙287∙400=646.3 кДж.

8.2. Определить количество теплоты , необходимое для нагревания 2000 м³ воздуха при постоянном давлении р=0.5 МПа от t₁=150°С до t₂=600°С. Зависимость теплоемкости от температуры считать нелинейной.

Ответ: Q_р=3937 МДж.

8.3. В установке воздушного отопления внешний воздух при t₁=-15°С нагревается в калорифере при р=const до 60°С. Какое количество теплоты надо затратить для нагревания 1000 м³ наружного воздуха? Теплоемкость воздуха считать постоянной. Давление воздуха принять равным 101 325 Па.

Отв. 103 МДж.

8.4. В цилиндре находится воздух при давлении р=0.5 МПа и температуре t₁=400°С. От воздуха отнимается теплота при постоянном давлении таким образом, что в конце процесса устанавливается температура t₂=0°С. Объем цилиндра , в котором находится воздух , равен 400 л.

Определить количество отнятой теплоты, конечный объем, изменение внутренней энергии и совершенную работу сжатия. Зависимость теплоемкости от температуры считать нелинейной.

Решение:

Количество отнятой теплоты по формуле

Q_p=V_нc”_pm(t_2-t1).

Объем воздуха при нормальных условиях определим из выражения

V_н=pVT_н/p_нT=0.5∙0.4∙273/0.1013∙673=0.8 м³.

По табл. 4.2, 4.3 находим

c’_pm=1.3289 кДж/м³ К.

Следовательно,

Q_p=0.8∙1.3289(0-400)=- 425кДж.

Это же количество теплоты можно вычислить не только по объему воздуха , но и по его массе:

Q_p=Mc_pm(t₂-t₁).

Массу воздуха определяем из характеристического уравнения

M=Р₁V₁/RT₁=0.5∙10⁶∙0.4/287∙673=1.035 кг.

Из табл. 4.2 находим

c_pm=1.0283 кДж/кг К.

Следовательно,

Q_p=1.035∙1.0283(0-400)=-425 кДж.

Конечный объем получим из уравнения (10.4)

V₂=V₁T₂/T₁=0.4∙273/673=0.1622 м³.

Изменение внутренней энергии

DU=V_нc’_vm(t₂-t₁).

Пользуясь табл. 4.2, находим

c’_vm=0.9579 кДж/м³ К.

Следовательно,

DU=0.8∙0.9579(0-400)=-306.5 кДж.

Работа, затраченная на сжатие, по формуле (8.4)

L=Р(V₂-V₁)=0.5∙10⁶(0.1622-0.4)=-118.9 кДж.

8.5. Для использования отходящих газов двигателя мощностью N=2500 кВт установлен подогреватель, через который проходит 60000 м³/ч воздуха при температуре t₁=15 °С и давлении Р=0.101 МПа. Температура воздуха после подогревателя равна 75 °С.

Определить, какая часть теплоты топлива использована в подогревателе? К.П.Д. двигателя принять равным 0.33. Зависимость теплоемкости от температуры считать линейной.

Ответ: 17.4%.

8.6. 2 м³ воздуха с начальной температурой t₁=15 °С расширяются при постоянном давлении до 3 м³ вследствие сообщения газу 837 кДж теплоты. Определить конечную температуру, давление газа в процессе и работу расширения.

Ответ: t₂=159°С, Р=0.24 МПа, L=239 кДж.

8.7. Отходящие газы котельной установки проходят через воздухоподогреватель. Начальная температура газов t_г1=300 °С, конечная t_г2=160 °С; расход газов равен 1000 кг/ч. Начальная температура воздуха составляет t_в1=15 °С, а расход его равен 910 кг/ч.

Определить температуру нагретого воздуха t_в2, если потери воздухоподогревателя составляют 4 %. Средние теплоемкости (c_pm) для отходящих из котла газов и воздуха принять соответственно равными 1,0467 и 1,0048 кДж/кг К.

Ответ: t_в2=168,9 °С.

8.8. Определить, какая часть теплоты, подводимой к газу в изобарном процессе, расходуется на работу и какая - на изменение внутренней энергии.

Решение:

Аналитическое выражение первого закона термодинамики

dq=du+dl

может быть представлено в виде

du/dq+dl/dq=1.

Величина

dl/dq=1-du/dq

определяет ту долю от всей подводимой к газу теплоты, которая превращается в работу расширения. Так как для идеального газа в процессе Р=const

du=c_vdt и dq=c_pdt,

то

dl/dq=1-c_vdt/c_pdt.

Принимая к=1.4, получаем

dl/dq=1-1/1.4=0.285.

Следовательно, в изобарном процессе только 28.5% теплоты, подводимой к газу, превращается в работу. Вся остальная теплота, т.е. 71.5%, расходуется на увеличение внутренней энергии.