Политропный процесс

Уравнение политропы в системе координат при постоянной теплоемкости

,

где - показатель политропы.

Характеристикой политропного процесса является величина

, (11.1)

которая может быть определена из выражения

, (11.2)

где .

Зависимости между начальными и конечными параметрами процесса:

между и , (11.3)

между и , (11.4)

между и 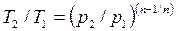. (11.5)

Работу 1 кг газа находят по следующим формулам:

; (11.6)

; (11.7)

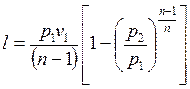; (11.8)

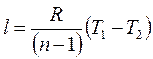. (11.9)

Если количество теплоты, участвующей в процессе, известно, то работа может быть также вычислена по формуле

. (11.10)

Для определения работы M кг газа нужно в формулах (11.6) – (11.8)заменить удельный объем v полным объемом V газа. Тогда получим

; (11.11)

; (11.12)

; (11.13)

Формулы (11.9) и (11.10) для M кг газа имеют следующий вид:

; (11.14)

. (11.15)

Теплоемкость политропного процесса можно найти из уравнения ,

или, заменяя его значением из уравнения (11.2), получим

.

Количество теплоты, сообщаемой газу или отнимаемой от него:

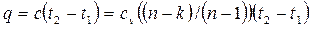(11.16)

(11.17)

Величину можно также определить из формулы (11.15), если известна работа политропного процесса:

. (11.18)

Изменение внутренней энергии газа в политропном процессе

. (11.19)

Показатель политропного процесса определяется из уравнения

. (11.20)

Задачи

11.1. 1 кг воздуха при р₁=0.5 МПа и t₁=111°С расширяется политропно до давления Р₂=0.1 МПа.

Определить конечное состояние воздуха, изменение внутренней энергии, количество подведенной теплоты и полученную работу, если показатель политропы n=1.2.

Решение:

Определяем начальный объем воздуха

v₁=RT₁/Р₁=(287∙384)/(0.5∙10⁶)=0.22 м³/кг.

Конечный объем воздуха находим из уравнения (11.3)

v₂=v₁(Р₁/Р₂)^1/n=0.22∙5^1/1.2=0.84 м³/кг.

Конечную температуру проще всего получить из характеристического уравнения

T₂=Р₂v₂/R=0.1∙10⁶∙0.84/287=293 K.

Величину работы находим из уравнения (10.9)

L=R(T₁-T₂)/(n-1)=287(384-293)/0.2=130 600 Дж/кг=130.6 кДж/кг.

Изменение внутренней энергии

Du=c_v(T₂-T₁)=20.93(293-384)/28.96=-65.8 кДж/кг.

Количество теплоты, сообщенной воздуху , по уравнению (11.17)

q=c_v(n - k)/(n - 1)·(t₂-t₁)=0.72(1.2-1.4)/(1.2-1) (20-111)=65.8 кДж/кг.

Нетрудно видеть, что в этом процессе внешняя работа совершается за счет подведенной теплоты и уменьшения внутренней энергии. Исходя из этого можно проверить полученные результаты следующим образом:

q=Du+L; L=q - Du=65.8-(-65.8)=131.6 кДж/кг.

Этот же результат получен выше другим путем.

11.2. 1.5 кг воздуха сжимают политропно от р₁=0.09 МПа и t₁=18°С до р₂=1 МПа, температура при этом повышается до t₂=125°С.

Определить показатель политропы, конечный объем, затраченную работу и количество отведенной теплоты.

Решение:

По формуле

(n-1)/n=(lgT₂/T₁)/(lgp₂/p₁)=(lg398/291)/(lg100/9)=0.13,

отсюда

n=1/(1-0.13)=1.149.

Конечный объем находим из характеристического уравнения

V₂=MRT₂/p₂=1.5∙287∙398/10⁶=0.171 м³.

Затраченная работа по уравнению (10.46)

L=MR(t₁-t₂)/(n-1)=1.5∙287(18-125)/0.149=-309200 Дж=-309.2 кДж.

Количество отведенной теплоты по уравнению

Q=Mc_v(n-k)/(n-1) (t₂-t₁)=

=1.5∙20.93/28.96∙(1.149-1.4)/(1.149-1) (125-18)=-195.4 кДж.

11.3. Воздух в количестве 3 м³ расширяется политропно от р₁=0.54 МПа и t₁=45°С до р₂=0.15 МПа. Объем, занимаемый при этом воздухом, становится равным 10 м³.

Найти показатель политропы, конечную температуру, полученную работу и количество подведенной теплоты.

Ответ: m=1.064, t₂=21.4°С, L=1875 кДж, Q=1575 кДж.

11.4. В цилиндре двигателя с изобарным подводом теплоты сжимается воздух по политропе с показателем m=1.33.

Определить температуру и давление воздуха в конце сжатия, если степень сжатия ( e=V₁/V₂) равна 14, t₁=77°С и р₁=0.1 МПа.

Ответ: t₂=564°С, р₂=3.39 МПа.

Знак плюс(+) показывает , что теплота в данном процессе подводится . Об этом можно судить также по величине показателя политропы.

Изменение внутренней энергии

DU= Q – L =672.4-1923=-1250.6 кДж.

Знак минус (-) показывает, что внутренняя энергия убывает . В данном процессе работа совершается за счет подводимой извне теплоты, а также внутренней энергии газа.

11.5. В процессе политропного сжатия затрачивается работа , равная 195 кДж, причем в одном случае от газа отводится 250 кДж, а в другом - газу сообщается 42 кДж.

Определить показатели обеих политроп.

Ответ: 1). m=0.9, 2). m=1.49.

11.6. 1.5 м³ воздуха сжимаются от 0.1 МПа и 17°С до 0.7 МПа, конечная температура при этом равна 100°С.

Какое количество теплоты требуется отвести, какую работу затратить и каков показатель политропы?

Ответ: Q=-183 кДж, L=-290 кДж, m=1.147.

11.7. 0.01 м³ воздуха при давлении р₁=1 МПа и температуре t₁=25°С расширяется в цилиндре с подвижным поршнем до 0.1 МПа.

Найти конечный объем, конечную температуру, работу, произведенную газом, и подведенную теплоту, если расширение в цилиндре происходит: а)изотермически, б)адиабатно и в)политропно с показателями m =1.3.

Решение:

а). Изотермическое расширение. Конечный объем определяют по формуле (11.11)

V₂=V₁p₁/p₂=0.01∙1/0.1=0.1 м³.

Так как в изотермическом процессе t=const, то конечная температура t₂=t₁=25°С.

Работа газа по уравнению (10.17)

L=p₁V₁lnp₁/p₂=1∙10⁶∙0.01∙2.303lg10=23 000 Дж.

Количество подведенной теплоты по формуле (11.19)

Q=L=23 кДж.

б). Адиабатное расширение. Конечный объем определяется по уравнению (11.20)

V₂=V₁(p₁/p₂)^1/k=0.01∙10^1/1.4.

Пользуясь табл. XIX, получаем 10^1/1.4=5.188.

Следовательно

V₂=0.01∙5.188=0.05188 м³.

Конечная температура воздуха на основании уравнения (11.22)

T₂=T₁(p₂/p₁)^k-1/k=298(0.1/1)^1.4-1/1.4=154.3 K; t₂=-118.7°С.

Работа газа по уравнению (10.29)

L=p₁V₁/(k-1) (1-(p₂/p₁)^k-1/k)=1∙10⁶∙0.01/0.4∙(1-1/1.931)=

=25000∙0.48=12 000Дж=12 кДж.

в). Политропное расширение. Конечный объем найдем из уравнения (11.35)

V₂=V₁(p₁/p₂)^1/m=0.01∙10^1/1.3=0.01∙5.885=0.05885 м³.

Конечная температура по уравнению (10.37)

T₂=T₁(p₁/p₂)^m-1/m=298(0.1/1)^0.3/1.3=175.2 K; t₂=-97.8 °С.

Работа газа по уравнению (10.45)

L=p₁V₁/(m-1) (1-(p₂/p₁)^m-1/m)=

=1∙10⁶∙0.01/0.3∙(1-(0.1/1)^0.3/1.3)=13700 Дж=13.7 кДж.

Подведенная теплота по уравнению (10.50)

Q=L(k-m)/(k-1)=13.7∙0.1/0.4=3.425 кДж.

11.8.В процессе политропного расширения воздуху сообщается 83.7 кДж тепла.

Найти изменение внутренней энергии воздуха и произведенную работу, если объем воздуха увеличился в 10 раз, а давление его уменьшилось в 8 раз.

Ответ: DU=16.7 кДж; L=6702 кДж.

11.10. Воздух расширяется по политропе, совершая при этом работу, равную 270 кДж, причем в одном случае ему сообщается 420 кДж теплоты, а в другом - от воздуха отводится 92 кДж теплоты.

Определить в обоих случаях показатели политропы.

Ответ: 1). m=0.78; 2). m=1.88.

11.11. 2 м³ воздуха при давлении р₁=0.09 МПа и температуре t₁=40°С сжимаются до давления р₂=1.1 МПа и объема V₂=0.5 м³.

Определить показатель политропы, работу сжатия и количество отведенной теплоты.

Ответ: m=1.23; L=-652 кДж; Q=-272 кДж.