Второй закон термодинамики

Второй закон термодинамики определяет направление, в котором протекают процессы, устанавливает условия преобразования тепловой энергии в механическую, а также определяет максимальное значение работы, которая может быть произведена тепловым двигателем.

Математически он может быть выражен следующим образом:

, (13.1)

где - бесконечно малое приращение энтропии системы;

- бесконечно малое количество теплоты, полученной системой от источника теплоты;

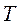- абсолютная температура источника теплоты.

Аналитическое выражение второго закона термодинамики для бесконечно малого обратимого процесса имеет вид

dQ=TdS , (13.2)

а так как, согласно первому закону термодинамики

dQ= dU+PdV

то уравнение (13.2) примет вид

TdS = dU+PdV

Основным уравнением для определения энтропии в обратимом процессе является выражение

ds=dq/T (13.3)

Определение энтропии для любого состояния газа, отсчитанной от нормального состояния производят по следующим формулам.

При переменной теплоемкости, исходя из линейной зависимости ее от температуры:

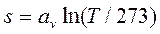
; (13.4)

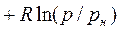
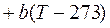; (13.5)

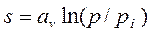
. (13.6)

При постоянной теплоемкости

; (13.7)

; (13.8)

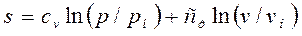(13.9)

Изменение энтропии между двумя произвольными состояниями газа 1 и 2 определяют по следующим формулам.

При переменной теплоемкости, считая зависимость ее от температуры линейной:

; (13.10)

; (13.11)

(13.12)

При постоянной теплоемкости ; (13.13)

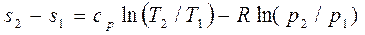; (13.14)

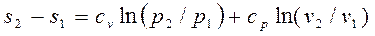. (13.15)

Если работа совершается с помощью газа, параметры которого отличаются от параметров окружающей среды, то максимальная работа, которую может произвести этот газ, достижима лишь при условии его перехода от начального состояния к состоянию среды обратимым путем.

При этом максимальная полезная работа меньше максимальной работы на величину работы вытеснения воздуха окружающей среды.

Величина максимальной полезной работы определяется формулой

. (13.16)

В этой формуле параметры, имеющие индекс 1 и 2, относятся соответственно к начальному и конечному состоянию источника работы, а параметры с индексом 0 относятся к рабочей среде.

Так как выражения 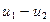и представляют собой соответственно абсолютную величину работы адиабатного и изотермического процесса, то формулу (6.16) можно представить в виде:

. (13.17)

Задачи

13.1. Определить энтропию 1 кг кислорода при р=0.8 МПа и t=250°С. Теплоемкость считать постоянной.

Решение:

По формуле (13.8)

s=C_pln(T/273)-R ln(p/p_н).

Так как для двухатомных газов mС_р=29.3 кДж/(кмоль К), а R=8.314 кДж/(кмоль К), то

s=29.3/32∙2.303∙lg(523/273)-8.314/32∙2.303∙lg(8/1.013);

s=0.5978-0.5373=0.0605 кДж/(кг К).

13.2. Найти энтропию 1 кг кислорода при р=0.8 МПа и t=250°С. Теплоемкость считать переменной , приняв зависимость ее от температуры линейной.

Решение:

По формуле (13.5)

s=a_pln(T/273)-Rln(p/p_н)+b(T-273).

Из табл. 5 для кислорода

С_pm=0.0127+0.00012724t кДж/(кг К).

Поэтому формула линейной зависимости истинной теплоемкости будет иметь вид

С_р=0.9127+0.00025448t кДж/(кг К),

или

С_р=0.8432+0.00025448Т кДж/(кг К).

Таким образом,

а=0.8432; b=0.00025448;

значение энтропии

s=0.8432∙2.303∙lg(523/273)-8.314/32∙lg(0.8/0.1013)+0.00025448∙(523-273);

s=0.5476-0.5371+0.0634=0.0739 кДж/(кг К).

Для тех же условий , но при постоянной теплоемкости (см. 1) значение энтропии s=0.0605 кДж/(кг К), т.е. меньше на

(0.0739-0.0605)/0.0739=0.0134/0.0739=18.1%.

Этот результат показывает, что для повышенных и высоких температур следует пользоваться зависимостью c=f(t).

13.3. 1 кг воздуха сжимается по адиабате так, что объем его уменьшается в 6 раз, а затем при v=const давление повышается в 1.5 раза.

Найти общее изменение энтропии воздуха. Теплоемкость считать постоянной.

Решение:

Изменение энтропии воздуха в адиабатном процессе будет равно нулю.

Изменение энтропии в изохорном процессе определится по формуле (13.13):

Ds_v=C_vlnT₃/T₂=C_vlnp₃/p₂=C_vln1.5=2.303∙20.93/28.96lg1.5=0.293 кДж/(кг К);

следовательно,

Ds=Ds_v=0.293 кДж/(кг К).

13.4. 1 кг воздуха сжимается от р₁=0.1 МПа и t₁=15°С до р₂=0.5 МПа и t₂=100°С.

Определить изменение энтропии. Теплоемкость считать постоянной.

13.5. 10 м3 воздуха , находящегося в начальном состоянии при нормальных условиях, сжимают до конечной температуры 400°С. Сжатие производится:1). изохорно, 2). изобарно, 3). адиабатно и 4). политропно с показателем политропы m=2.2.

Считая значение энтропии при нормальных условиях равным нулю и принимая теплоемкость воздуха постоянной, найти энтропию воздуха в конце каждого процесса.

Решение:

Находим массу 10 м3 воздуха при нормальных условиях:

M=pV/RT=0.1013∙10⁶∙10/287∙273=12.9 кг.

Определяем изменение энтропии в каждом из перечисленных процессов:

1). изохорное сжатие

Ds₁=s₁=Mc_vlnT/273=12.9 0.723 2.303lg673/273=8.42 кДж/К;

2). изобарное сжатие

Ds₂=s₂=Mc_plnT/273=12.9 1.0117 2.303lg673/273=11.7 кДж/К;

3). адиабатное сжатие

Ds₃=s₃=0;

4).политропное сжатие

Ds4=s4=Mcv(m-k)/(m-1)lnT/273=

=12.9 0.723(2.2-1.4)/(2.2-1) 2.303lg673/273=5.61 кДж/К.

13.6. Найти приращение энтропии 3 кг воздуха) при нагревании его по изобаре от 0 до 400°С; б) при нагревании его по изохоре от 0 до 880°С; в) при изотермическом расширении с увеличением объема в 16 раз. Теплоемкость считать постоянной.

Ответ: а) Ds_p=2.74; б) Ds_v=3.13; в) Ds_t=2.36 кДж/К.

13.7. 1 кг воздуха сжимается по политропе от 0.1 МПа и 20°С до 0.8 МПа при m=1.2. Определить конечную температуру , изменение энтропии, количество отведенной теплоты и затраченную работу.

Ответ: t₂=141°С; Ds=-0.2445 кДж/кг К; q=-87.1 кДж/кг; l=-173 кДж/кг.

13.8. В процессе политропного расширения воздуха температура его уменьшилась от t₁=25°С до t₂=-37°С. Начальное давление воздуха р₁=0.4 МПа, количество его М=2 кг. Определить изменение энтропии в этом процессе, если известно, что количество подведенной к воздуху теплоты составляет 89.2 кДж.

Решение:

Количество теплоты, сообщаемое газу в политропном процессе составляет:

Q=Mc_v(m-k)/(m-1) (t₂-t₁).

Подставляя значения известных величин, получаем

(m-k)/(m-1)=-89.2/(2 0.723 62)=-0.995.

Отсюда показатель политропы m=1.2.

Из соотношения параметров политропного процесса определяем конечное давление:

p₂/p₁=(T₂/T₁)^m/(m-1); p₂=p₁(T₂/T₁)^m/(m-1)=4(236/298)⁶=0.1 МПа.

Изменение энтропии по уравнению

Ds=M(c_plnT₂/T₁-Rlnp₂/p₁);

следовательно,

Ds=2·2.3(29.3/28.96∙lg236/298-287/1000∙lg0.1/0.4)=

=4.6(-0.1026+0.1728)=0.323 кДж/К.

13.9. В сосуде объемом 400 л заключен воздух при давлении р₁=0.1 МПа и температуре t₁=-40°С. Параметры Среды р₀=0.1 МПа и t₀=20°С.Определить максимальную полезную работу , которую может произвести воздух, заключенный в сосуде. Представить процесс в диаграммах pv и Ts.

Ответ: L_max(_полезн) =4600 Дж.