Прямые общего положения на чертеже. Решение с ними метрических задач

Прямая общего положения расположена произвольно относительно основных плоскостей проекций, а её проекции образуют с линиями связи углы, отличные от 0 и 90 .

Любая проекция отрезка такой прямой всегда меньше самого отрезка (свойство ортогонального проецирования). Поэтому определение по чертежу истинной величины отрезка прямой общего положения (решение первой основной метрической задачи ОМЗ.1) осуществляется путём дополнительных построений.

Если рассмотреть (рис. 3.9) процесс проецирования некоторого отрезка АВ на какую либо плоскость проекций, например, на плоскость 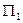, то очевидно, что отрезок АВ и его проекция AB образуют горизонтально проецирующую плоскость.

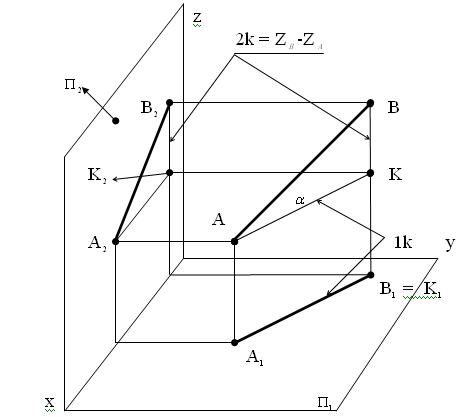
Рис. 3.9

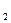Проведя в этой плоскости прямую АК || A B, мы получим прямоугольный треугольник АВК, у которого один катет - АК (назовём его первым) равен проекции A B , другой - ВК (назовём его вторым) равен разности расстояний концов отрезка до плоскости проекции A B (Z - Z ), величина которой определяется с помощью фронтальной проекции A B 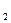. Гипотенуза этого прямоугольника есть сам отрезок АВ в истинную величину. 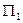Угол между гипотенузой и первым катетом (проекцией A B ) есть угол наклона заданного отрезка к плоскости проекции (угол ).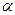

Для сокращения графической работы рассмотренный прямоугольник строят на комплексном чертеже отрезка (рис. 3.10), обычно на соответствующей его проекции (на первом катете).

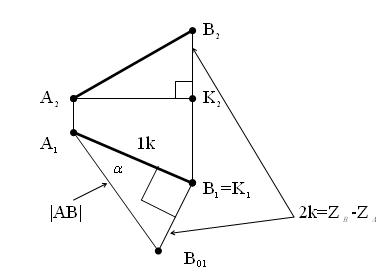
Рис. 3.10

Этот способ определения истинной величины отрезка прямой общего положения и угла его наклона к плоскости проекций получил название метод прямоугольного треугольника.

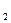Решим задачу (рис. 3.11). Заданы проекции отрезка: А В и А В 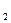. Определить угол наклона отрезка АВ к профильной плоскости проекций (угол ).

Рис. 3.11

Алгоритм решения:

1. Строится профильная проекция А В .

2. На базе проекции А В , как на первом катете, строится вспомогательный прямоугольник А В А .

3. Искомый угол - угол между гипотенузой А В и первым катетом А В .