Разновидности плоских поверхностей

Различают плоские поверхности простые и составные.

Простые плоские поверхности бывают двух видов: плоскости и грани.

Плоскость - неограниченная плоская поверхность. На чертеже её

задают изображением элементов определителя.

Плоскость моделируют как траекторию непрерывного перемещения прямой образующей (прямолинейного или вращательного вокруг оси, перпендикулярной образующей прямой).

Перемещение образующей можно задавать следующим образом.

1) Параллельными прямыми - (l, a || b).

2) Двумя пересекающимися прямыми - (l, a b).

3) Вращением вокруг оси, перпендикулярной образующей прямой - (l i).

4) Точкой и прямой - (l, A, b). Этот вариант может быть преобразован в любой из первых трёх.

Грань - плоскость, ограниченная замкнутой линией. На чертеже грань изображают линиями её границ (контуром, очерком).

На рис. 5.1 – 5.3 представлены изображения граней: треугольника, четырёхугольника и круга.

Рис. 5.1

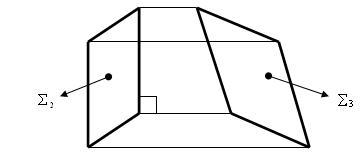
Рис. 5.2

Рис. 5.3

Составные плоские поверхности (многогранные) – представляют собой несколько граней (не лежащих в одной плоскости), состыкованных между собой. Линию стыка каждой пары граней называют рёбром, которое является общей линией границ этих граней (их общей образующей).

Составные плоские поверхности подразделяют на монотипные и комплексные многогранные поверхности.

Монотипные многогранные поверхности моделируют с помощью направляющей ломаной прямой линии. При этом различают следующие варианты таких поверхностей.

Призматическая поверхность. Моделирование призматической поверхности производят путём параллельного перемещения образующей прямой l по направляющей ломаной прямой m (все рёбра между собой параллельны).

На рис. 5.4 представлен аксонометрический чертёж призматической поверхности.

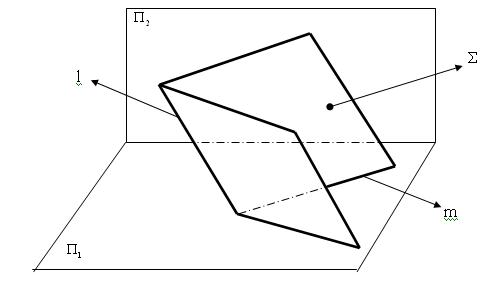
Рис. 5.4

Комплексный чертёж определителя призматической поверхности представлен на рис. 5.5.

Рис. 5.5

Комплексный чертёж призматической поверхности выполнен на рис. 5.6.

Рис. 5.6

Частным случаем призматической поверхности является призма, которая представляет собой замкнутую призматическую поверхность (направляющая ломаная прямая – замкнута).

На рис. 5.7 приведён чертёж прямой трёхгранной призмы.

Рис. 5.7

Пирамидальная поверхность. Поверхность моделируется перемещением прямой образующей l по ломаной направляющей прямой m , когда другой её конец остаётся в точке S - вершине призматической поверхности (все рёбра пересекаются в одной точке).

На рис. 5.8 представлен комплексный чертёж пирамидальной поверхности.

Рис. 5.8

Частным случаем пирамидальной поверхности является пирамида, которая представляет собой замкнутую пирамидальную поверхность (направляющая ломаная прямая – замкнута).

На рис. 5.9 представлен комплексный чертёж трёхгранной пирамиды.

Рис.5.9

Комплексные многогранные поверхности получают стыковкой многогранных поверхностей и граней разного типа.