
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение по чертежу положения плоскостей относительно основных плоскостей проекций
По расположению рассматриваемых плоскостей относительно основных плоскостей проекций различают плоскости частного и общего положения.
Плоскости частного положения разделяют на следующие два типа.
1. Проецирующая плоскость, перпендикулярная какой-либо из основных плоскостей проекций.
2. Плоскость уровня, параллельная какой-либо плоскости проекций.
Проецирующая плоскость на перпендикулярной ей плоскости проекций изображается в виде прямой линии, т.е. геометрической фигурой на единицу меньшего измерения. Эту проекцию принято называть главной проекцией проецирующей плоскости. Здесь же без искажения изображены и углы её наклона к другим плоскостям проекций.
Среди проецирующих плоскостей различают следующие плоскости.
Горизонтально проецирующая плоскость (рис. 5.10).

Рис. 5.10
Фронтально проецирующая плоскость (рис. 5.11).
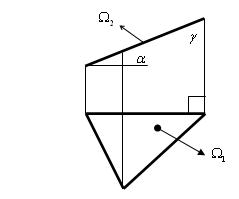
Рис. 5.11
Профильно проецирующая плоскость (рис. 5.12).

Рис. 5.12
На чертеже проецирующей плоскости определены углы её наклона к основным плоскостям проекций.
Среди плоскостей уровня различают следующие плоскости.
Горизонтальная плоскость (рис. 5.13).

Рис.5.13
Фронтальная плоскость (рис. 5.14).
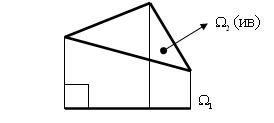
Рис. 5.14
Профильная плоскость (рис. 5.15).

Рис. 5.15
Проекция плоскости уровня на плоскость проекций, которой она не параллельна, а, следовательно, перпендикулярна, изображается прямой, перпендикулярной линиям связи с параллельной плоскостью проекций. Эту проекцию принято называть главной и определяющей.
На плоскости проекций, которой параллельна грань, определены истинная форма грани и её площадь.
Плоскости общего положения (относительно основных плоскостей проекций) на чертеже изображаются с искажением их метрических параметров (например, длин отрезков, углов их наклона к плоскостям проекций) и для определения этих параметров требуются дополнительные построения.
Например, если необходимо определить угол наклона заданной плоскости общего положения  (рис. 5.16) к плоскости проекций
(рис. 5.16) к плоскости проекций 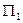 (угол
(угол 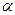 ), то для этого используют так называемую “линию (прямую) наклона” плоскости
), то для этого используют так называемую “линию (прямую) наклона” плоскости  к плоскости проекций
к плоскости проекций 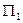 .
.

Рис. 5.18
Эту прямую обозначают буквой g 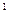 и она пересекает горизонтали заданной плоскости под прямым углом (на горизонтальную плоскость проекций этот прямой угол проецируется без искажения).
и она пересекает горизонтали заданной плоскости под прямым углом (на горизонтальную плоскость проекций этот прямой угол проецируется без искажения).
Теперь, если на прямой g 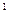 взять отрезок, то с помощью этого отрезка, используя метод «прямоугольного треугольника», можно определить угол наклона прямой g
взять отрезок, то с помощью этого отрезка, используя метод «прямоугольного треугольника», можно определить угол наклона прямой g 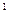 к плоскости проекций
к плоскости проекций 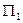 , а это значит и угол наклона заданной плоскости
, а это значит и угол наклона заданной плоскости  к плоскости проекций
к плоскости проекций 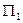 (угол
(угол 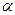 ).
).
Для определения углов наклона плоскости  к другим плоскостям проекций (
к другим плоскостям проекций (  и
и  ) на заданной плоскости строят соответствующие прямые линии наклона g
) на заданной плоскости строят соответствующие прямые линии наклона g 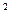 и g
и g  , которые перпендикулярны соответственно фронталям и профильным прямым.
, которые перпендикулярны соответственно фронталям и профильным прямым.
Решим задачу (рис. 5.17). Через точку В  (ABC) провести линию наклона g
(ABC) провести линию наклона g 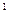 и определить угол наклона заданной плоскости
и определить угол наклона заданной плоскости  к горизонтальной плоскости проекций
к горизонтальной плоскости проекций 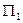 .
.

Рис. 5.19
Алгоритм решения.
1.В 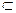 g
g 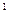
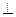 h = AC
h = AC  В
В 
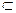 g
g 
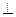 A
A  C
C  .
.
2.g 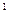
 AC = D
AC = D  g
g  = B
= B 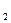 D
D  .
.
3.Угол 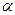 определяют методом прямоугольного треугольника на базе
определяют методом прямоугольного треугольника на базе
первого катета B  D
D  .
.
5.3. Определение по чертежу принадлежности плоской поверхности её элементов
Процесс определения принадлежности связан с решением позиционных задач второго типа ( ПЗ.2 ). На чертеже точку и линию, принадлежащих поверхности, можно задать (определить), только связав их с другими элементами этой поверхности, изображёнными на чертеже.
Правила определения принадлежности
1.Точка принадлежит плоскости, если она принадлежит какой-либо прямой линии этой плоскости.
2.Линия принадлежит плоскости, если она проходит через соответствующие точки этой плоскости. Точек должно быть достаточно для вычерчивания проекций рассматриваемой линии (например, прямая должна проходить через две точки этой плоскости или через одну точку, но в известном направлении).
Пример (рис. 5.20). Построить недостающие проекции точек M и D
и D , расположенных в плоскости треугольника
, расположенных в плоскости треугольника  (ABC). Провести через точку D в плоскости заданного треугольника прямую a || AB.
(ABC). Провести через точку D в плоскости заданного треугольника прямую a || AB.
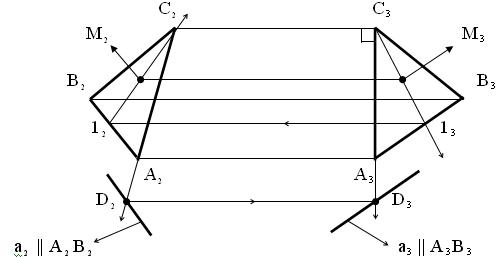
Рис. 5.20
Алгоритм решения
1. M  C
C 
 M
M  C
C  ;
;
2. D  A
A  C
C 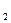
 D
D  A
A  C
C  ;
;
3. D  a
a 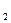 || A
|| A 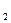 B
B 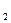 , D
, D  a
a  || A
|| A  B
B 
 AB || a
AB || a  .
.
Дата добавления: 2014-12-03; просмотров: 316; Мы поможем в написании вашей работы!; Нарушение авторских прав |