Кривые линии на чертеже

Кривая линия, как и прямая, - это простейшая геометрическая фигура (элемент моделирования), которую можно представить, как траекторию непрерывного движения точки по определённому закону. Построение кривых линий на чертеже производят с помощью достаточно большого числа её точек.

Различают плоские и пространственные кривые линии. Чтобы определить по чертежу вид кривой, необходимы дополнительные построения (рис. 4.1). Если на заданной кривой m взять 4 произвольные точки A , B , C , D , то, соединив эти точки хордами АС и BD, можно получить 2 варианта:

Рис. 4.1

1. Хорды пересекаются. Это значит, что они образуют плоскость, в которой лежит заданная кривая, т.е. эта кривая - плоская.

2. Хорды не пересекаются, а скрещиваются. Это значит, что заданная кривая – пространственная кривая.

В нашем примере кривая – пространственная.

Среди пространственных кривых широко известна в машиностроении цилиндрическая винтовая линия (рис. 4.2). Она моделируется траекторией непрерывного сложного движения образующей точки: вращательного (при постоянном радиусе и скорости) и поступательного параллельно оси вращения (тоже с постоянной скоростью). Расстояние, на которое переместится образующая точка вдоль оси вращения за один оборот, называют ходом винтовой линии.

Рис.4.2

Примером плоских кривых линий являются: окружность, эллипс, парабола, гипербола. Эти кривые описываются уравнениями второго порядка и поэтому их называют кривые второго порядка.

Плоские кривые (рис. 4.3), составленные из нескольких сопрягаемых дуг кривых линий различных уравнений называют обводами (обводы корпуса корабля, яхты, лодки).

Рис. 4.3. Обводы судна

Если плоские кривые линии составлены из сопряжённых дуг окружностей различных радиусов, то их называют коробовыми.

Решим задачу (рис. 4.4): через заданные точки A, B, C, D провести коробовую линию.

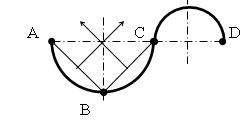
Рис. 4.4. Коробовая линия

Замкнутые коробовые кривые линии, имеющие не более двух точек пересечения с произвольной прямой, называются овалами (рис. 4.5).

Рис. 4.5. Овал

Свойства проекций кривых

1. Если точка принадлежит кривой линии, то проекции этой точки принадлежат проекциям кривой.

2. Секущая и касательная к плоской кривой проецируются соответственно в секущую и касательную к проекции кривой.

3. Плоская кривая проецируется в линию того же порядка. Например, проекция окружности - эллипс или окружность, проекция параболы - парабола.