
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пересечение плоских поверхностей на чертеже
Решение задач 2.ГПЗ. 1 ( 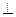 ,
, 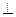 )
)
Алгоритм решения
1.Искомые проекции линии пересечения проецирующих плоскостей уже изображены на чертеже по принадлежности их главным проекциям.
2.Определяют видимость элементов геометрических фигур.
Пример (рис. 5.29). Построить трёх картинный чертёж пересекающихся проецирующих граней 
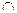
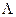 .
.

Рис. 5.29
Алгоритм решения:
1. 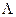
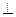
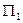

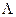
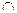
 = 12
= 12  1
1  2
2 
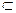
 ;
;
1 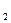 2
2 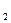
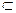
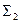 ;
;
1  2
2 
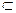
 .
.
Решение задач 2.ГПЗ . 2 ( 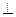 , не
, не 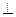 )
)
Алгоритм решения
1.Одна из искомых проекций линии пересечения геометрических фигур уже изображена на чертеже по её принадлежности главной проекции проецирующей фигуры.
2.Вторую проекцию строят по признаку её принадлежности геометрической фигуре общего положения.
3.Определяют видимость элементов заданных фигур.
Пример (рис. 5.30). Построить линию пересечения граней: m =  .
.

Рис. 5.30
Алгоритм решения:
1. 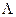
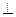

 m
m 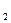 =
= 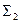 ;
;
m 
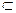
 .
.
Решение задач 2.ГПЗ . 3 (не 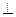 , не
, не 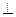 )
)
Эти главные позиционные задачи решают с использованием метода введения дополнительной плоскости – посредника.
Следует отметить, что пересечение плоских поверхностей любой сложности всегда сводится к рассмотрению пересечения каждой пересекающейся пары граней этих поверхностей.
Рассмотрим последовательность построения линии пересечения двух плоскостей (граней).
Алгоритм решения
1.Строят вспомогательную проецирующую плоскость – посредник так, чтобы она пересекла обе заданные геометрические фигуры.
2.Определяют обе линии пересечения посредника с заданными геометрическими фигурами, т.е. решают две задачи 2. ГПЗ. 2.
3.Определяют точки пересечения построенных линий. Эти точки – общие для заданных геометрических фигур.
4.Для получения необходимой второй точки линии пересечения заданных поверхностей вводится ещё одна проецирующая плоскость – посредник. По полученным двум точкам строят искомую линию пересечения.
5.Определяют видимость элементов заданных геометрических фигур.
Пример (рис. 5.31). Построить линию пересечения грани  с пирамидой: m =
с пирамидой: m =  .
.
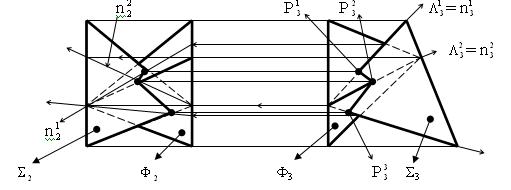
Рис. 5.31
Алгоритм решения:
1.  = n
= n  P
P 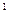 ;
; 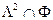 = n
= n 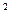
 P
P 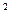 ;
;  = n
= n  P
P  ;
;
2.  = m = P
= m = P 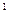 P
P 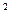 P
P  .
.
Дата добавления: 2014-12-03; просмотров: 310; Мы поможем в написании вашей работы!; Нарушение авторских прав |