Основные разновидности кривых поверхностей

1. Кривые поверхности с прямолинейными образующими (линейчатые поверхности)

1.1.Цилиндрическая поверхность

Цилиндрическая поверхность моделируется параллельным движением образующей прямой по направляющей кривой (плоской или пространственной). На рис. 6.3а представлен её аксонометрический чертёж, на рис. 6.3б – комплексный чертёж определителя этой поверхности, а на рис. 6.3в – чертёж самой поверхности.

Рис. 6.3

Частный случай цилиндрической поверхности - цилиндр вращения (рис. 6.4).

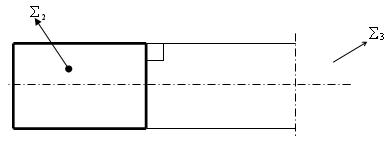
Рис. 6.4

1.2. Коническая поверхность

Коническая поверхность моделируется образующей прямой, проходящей через общую точку (вершину) и перемещающейся по направляющей кривой (плоской или пространственной). Её Аксонометрический чертёж такой поверхности представлен на рис.6.5а, комплексный чертёж её определителя – на рис. 6.5б, чертёж очерка конической поверхности – на рис. 6.5в .

Рис. 6.5

Частный случай конической поверхности – конус вращения (рис. 6.6).

Рис 6.6

1.3. Поверхности вращения с прямолинейными образующими

В зависимости от взаимного положения образующей и оси вращения различают следующие варианты поверхностей.

1. Цилиндр вращения (l || i), представленный на рис. 6.7).

2. Конус вращения (l 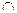i), см. рис. 6.8.

3. Однополостный гиперболоид вращения (l i), см. рис. 6.9.

Рис. 6.7

Рис. 6.8

Рис. 6.9

1.5. Винтовые поверхности с прямолинейными образующими (геликоиды)

Эти поверхности моделируют винтовым движением образующей, пересекающей направляющие: винтовую линию и ось вращения. Образующая совершает при этом сложное движение: вращательное вокруг оси и поступательное вдоль оси, одновременно.

Если угол между образующей и осью вращения равен 90 , то при моделировании получают прямой геликоид, у которого имеется плоскость параллелизма, перпендикулярная оси вращения. Все образующие косого геликоида параллельны этой плоскости.

Если угол между образующей и осью вращения не равен 90 , то получают косой геликоид, у которого имеется конус параллелизма. Все образующие этого конуса вращения параллельны соответствующим образующим косого геликоида. Пример косого геликоида представлен на рис. 6.10.

Винтовые поверхности используют при образовании резьбовых поверхностей деталей машин.

2. Поверхности вращения с криволинейной образующей

Рассмотрим такую поверхность общего вида (рис. 6.11). Обратим внимание на то, что при вращении образующей линии l каждая её точка описывает траекторию в виде окружности. Для удобства описания построения поверхности и решения с ней задач вводят собственные названия для некоторых линий поверхности:

1. Параллель a – траекторная окружность какой-либо точки образующей l.

2. Экватор b – параллель с наибольшим радиусом.

3. Горло c – параллель с наименьшим радиусом.

4. Меридиан l – образующая линия. Главный меридиан - меридиан, лежащий в плоскости, параллельной какой-либо основной плоскости проекций.

Примечание: при изображении таких поверхностей удобно располагать их так, чтобы относительно основных плоскостей проекций ось вращения занимала проецирующее положение.

Рис. 6.10

Рис. 6.11

Частные разновидности поверхностей вращения

Это поверхности, получаемые вращением плоской кривой образующей второго порядка (окружности, эллипса, параболы и гиперболы) вокруг оси, лежащей в плоскости образующей кривой.

1. Торовая поверхность

Торовая поверхность моделируется вращением вокруг оси образующей окружности или её дуги.

Разновидности торовых поверхностей:

Сфера (m, i = d), представленная на рис. 6.12.

Рис. 6.12

Кольцо (m, i d), см. рис. 6.13.

Рис. 6.13

Галтель (m, i), см. рис. 6.14.

Рис. 6.14

2.Эллипсоид вращения

Эллипсоид вращения моделируется вращением вокруг своей оси образующего эллипса.

Различают:

2.1. Сжатый эллипсоид (m, i), см. рис. 6.15.

Рис. 6.15

2.2. Вытянутый эллипсоид (m, i), см. рис. 6.16.

Рис. 6.16

3. Параболоид вращения

Параболоид вращения (рис. 6.17), моделируется вращением образующей параболой вокруг её оси.

Рис. 6.17

4. Гиперболоид вращения

Различают:

4.1.Однополостный гиперболоид вращения (m, i), у которого образующая гипербола вращается вокруг её действительной оси (рис. 6.18).

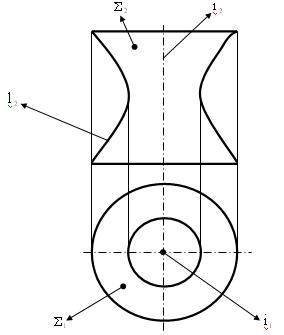
Рис. 6.18

4.2. Двухполостный гиперболоид вращения (m, i), у которого образующая гипербола вращается вокруг её мнимой оси (рис. 6.19).

Рис. 6.19

2. Каналовые поверхности

Эти поверхности моделируются замкнутым плоским контуром (прямолинейным или криволинейным), который перемещается своим центром по направляющей линии. При этом угол между направляющей и плоскостью образующего контура остаётся постоянным (например, 90 ). Образующий контур при перемещении может оставаться неизменным или изменять свои размеры, оставаясь подобным исходному контуру.

Аксонометрический чертёж такой поверхности представлен на рис. 6.20.

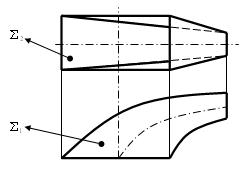
Рис. 6.20

Каналовые поверхности с неизменным образующим контуром называют трубчатыми (рис. 6.21).

Рис. 6.21

Частным случаем каналовых поверхностей являются циклические каналовые поверхности, у которых образующим контуром является окружность или эллипс (рис. 6.22).

Рис. 6.22

6.2. Принадлежность кривой поверхности её элементов на чертеже

Как для любой поверхности, так и для кривой справедливы рассмотренные выше правила определения принадлежности:

1.Точка принадлежит поверхности, если она принадлежит какой-либо линии этой поверхности, удобной для изображения её на чертеже (например, прямой линии или окружности).

2.Линия принадлежит поверхности, если она проходит через соответствующие точки этой поверхности. Точек должно быть достаточно для вычерчивания проекций рассматриваемой линии.

Пример (рис. 6.23). Построить недостающие профильные проекции линий m и n, а также точек А и В на сфере .

Рис. 6.23

Профильные проекции точек А и В определяем по принадлежности их соответственно главному фронтальному и главному профильному меридианам.

Так как проекции m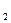и n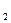 выглядят, как отрезки ломаной прямой, то это значит, что линии m и n представляют собой две дуги окружностей, соединённых в ломаную окружность в точке А. Плоскости этих дуг окружностей занимают фронтально проецирующее положение. Плоскость дуги n параллельна профильной плоскости проекций, поэтому на ней дуга n изобразится в истинную величину. Плоскость дуги m не параллельна профильной плоскости проекций, поэтому проекция на неё m представляет собой дугу эллипса. Эту проекцию строят по точкам, выбранным на фронтальной проекции m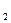, привязывая их к параллелям и меридианам заданной сферы.