
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Взаимное пересечение кривых поверхностей на чертеже (2.ГПЗ)
Решение задач 2.ГПЗ. 1 (  ,
,  )
)
Алгоритм решения
1.Искомые проекции линии пересечения проецирующих геометрических фигур уже изображены на чертеже по принадлежности их главным проекциям.
2.Определяют видимость элементов геометрических фигур.
Пример. Рассмотреть варианты пересечения кривых поверхностей на базе проецирующих цилиндров вращения. Результатом пересечения, в общем случае, являются пространственные кривые линии.
Вариант 1 (рис. 6.36). Проницание: m  =
=  .
.

Рис. 6.36
Вариант 2 (рис. 6.37). Вмятие: n =  .
.
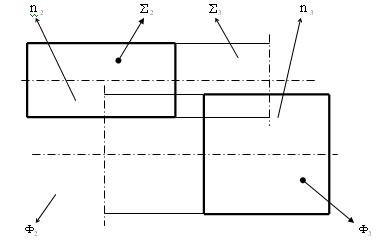
Рис. 6.37
Вариант 3 (рис. 6.38). Проницание с касанием: k =  .
.

Рис. 6.38
Решение задач 2.ГПЗ . 2 ( 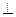 , не
, не 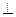 )
)
Алгоритм решения:
1.Одна из искомых проекций линии пересечения геометрических фигур уже изображена на чертеже по её принадлежности главной проекции проецирующей фигуры.
2.Вторую проекцию строят по признаку её принадлежности геометрической фигуре общего положения.
3.Определяют видимость элементов заданных фигур.
Пример (рис. 6.39). Построить проекции линии проницания с касанием m при пересечении сферы 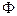 с цилиндром вращения
с цилиндром вращения  , если
, если 
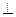
 .
.
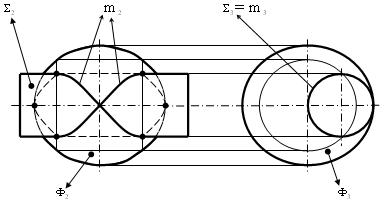
Рис. 6.39
Алгоритм решения.
1. m  =
=  .
.
2. На профильной проекции линии пересечения фигур выбираем несколько её точек (1 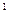 , 1
, 1 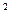 , 2, 3
, 2, 3 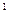 , 3
, 3 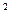 , 4
, 4 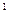 , 4
, 4 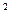 ). Строим их фронтальные проекции (по принадлежности точек сфере). Через построенные проекции точек проводим кривую линию (с учётом видимости её частей), являющейся проекцией m
). Строим их фронтальные проекции (по принадлежности точек сфере). Через построенные проекции точек проводим кривую линию (с учётом видимости её частей), являющейся проекцией m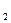 .
.
Решение задач 2.ГПЗ . 3 (не 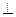 , не
, не 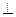 )
)
Эти главные позиционные задачи решают, применяя дополнительные построения. Чаще всего используют при этом метод введения дополнительных плоскостей – посредников.
Алгоритм решения
1.Строят вспомогательную проецирующую плоскость - посредник так, чтобы она пересекала обе заданные геометрические фигуры (поверхности).
2.Определяют обе линии пересечения посредника с заданными поверхностями, т.е. решают две задачи 2. ГПЗ. 2.
3.Определяют точки пересечения построенных линий. Эти точки - общие для заданных геометрических фигур.
4.Для получения достаточного числа общих точек пересекающихся фигур определяют и строят необходимое количество посредников. По полученным точкам строят искомую линию пересечения.
5.Определяют видимость элементов заданных геометрических фигур.
В данном разделе рассматривается порядок расчёта 2.ГПЗ.3 с пересекающимися поверхностями вращения.
Степень сложности решения этих задач зависит от взаимного положения осей вращения пересекающихся поверхностей.
Возможны следующие четыре варианта взаимного положения осей:
1.Оси вращения поверхностей совпадают: i 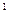 = i
= i 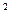 .
.
2.Оси параллельны: i 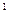 || i
|| i 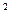 .
.
3.Оси пересекаются: i 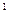
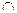 i
i 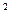 .
.
4.Оси вращения являются скрещивающимися прямыми: i 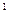
 i
i 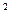 .
.
Рассмотрим примеры решения некоторых задач подобного типа.
Пример 1(рис. 6.40). Построить линию пересечения m полусферы 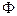 с конусом вращения
с конусом вращения  . Их оси вращения i
. Их оси вращения i 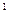 и i
и i 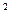 совпадают.
совпадают.
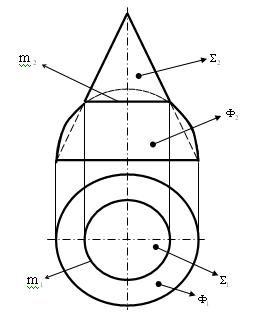
Рис. 6.40
Решение
Линиями пересечения таких поверхностей являются общие параллели, т.е. траектории вращения общих точек образующих заданных поверхностей.
Пример 2 (рис. 6.41). Построить линию пересечения полусфер  и
и 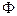 , у которых оси вращения i
, у которых оси вращения i 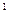 и i
и i 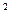 параллельны.
параллельны.
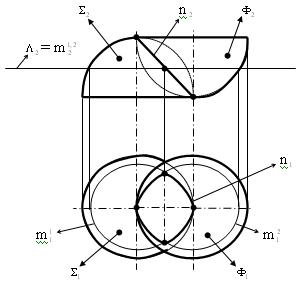
Рис. 6.41
Решение
Задачу решаем с использованием дополнительных проецирующих плоскостей - посредников, перпендикулярных осям вращения заданных полусфер. При этом задача сводится к решению нескольких задач типа 2.ГПЗ.2.
Плоскости - посредники рассекают заданные поверхности по параллелям. Точки пересечения параллелей являются искомыми общими точками заданных поверхностей (например, точки P 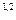 параллелей m
параллелей m 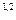 ). Через построенные точки A,B,P
). Через построенные точки A,B,P 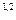 , … проводим искомую линию пересечения заданных поверхностей - n.
, … проводим искомую линию пересечения заданных поверхностей - n.
Пример 3(рис. 6.42). Построить линию пересечения конуса  с цилиндром вращения
с цилиндром вращения 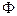 , если их оси i
, если их оси i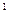 и i
и i пересекаются.
пересекаются.
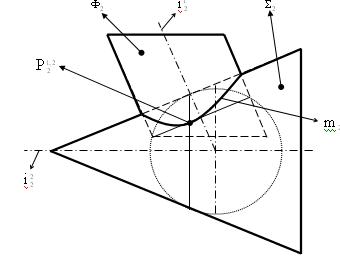
Рис. 6.42
Решение
Для решения подобных задач вместо проецирующих плоскостей-посредников рациональнее использовать концентрические секущие сферы-посредники с центрами в точке пересечения осей вращения заданных поверхностей.
Концентрические сферы пересекают заданные фигуры по параллелям - окружностям. При этом задача сводится к решению нескольких задач с поверхностями вращения, у которых совпадают оси вращения
(смотри ранее рассмотренный Пример 1).
Точки пересечения построенных параллелей являются искомыми общими точками заданных фигур: точками линии их пересечения.
Особенности решения задач на пересечение поверхностей вращения, описанных вокруг сферы (теорема Г. Монжа)
Две поверхности вращения второго порядка в общем случае пересекаются по пространственной кривой четвёртого порядка. Однако в некоторых частных случаях эта кривая распадается на две плоские кривые второго порядка. Известный французский геометр Г. Монж доказал следующую теорему: Если две поверхности вращения описаны вокруг сферы, то результатом их взаимного пересечения являются две плоские кривые второго порядка.
Пример (рис. 6.43). Построить фронтальные проекции линий пересечения двух цилиндров  и
и  , описанных вокруг сферы
, описанных вокруг сферы  .
.

Рис. 6.43
Решение
Плоскости кривых линий пересечения фигур m проходят через прямую, соединяющую точки двойного соприкосновения. Точками двойного соприкосновения называют 2 точки, в которых сфера одновременно касается обеих поверхностей. В нашем случае точками двойного соприкосновения являются точки А и В. Они определяются как точки пересечения окружностей a
проходят через прямую, соединяющую точки двойного соприкосновения. Точками двойного соприкосновения называют 2 точки, в которых сфера одновременно касается обеих поверхностей. В нашем случае точками двойного соприкосновения являются точки А и В. Они определяются как точки пересечения окружностей a 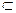
 и b
и b 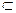
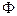 , по которым цилиндры касаются вписанной сферы
, по которым цилиндры касаются вписанной сферы 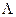 . Плоскости кривых пересечения фигур m
. Плоскости кривых пересечения фигур m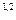 занимают фронтально - проецирующее положение и проходят через точки пересечения главных меридиан, т.е. через точки C, D, E, F. Линии пересечения заданных фигур m
занимают фронтально - проецирующее положение и проходят через точки пересечения главных меридиан, т.е. через точки C, D, E, F. Линии пересечения заданных фигур m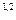 являются эллипсами.
являются эллипсами.
Дата добавления: 2014-12-03; просмотров: 335; Мы поможем в написании вашей работы!; Нарушение авторских прав |