Магнитные моменты электронов и атомов.

Опыт показывает, что магнитное поле действует не только на проводники с током, но и на отдельные заряды, движущиеся в магнитном поле. Сила, действующая на заряд q ,движущийся в магнитном поле со скоростью , называется силой Лоренца.

Опытным путем установлено, что

.

Направление силы Лоренца определяется для положительных зарядов правилом левой руки (т.к. направление и для совпадают): если ладонь левой руки расположить так, чтобы вектор входил в нее, а 4 вытянутых пальца сонаправить с движением положительного заряда, то отогнутый большой палец покажет направление силы Лоренца (рис. 9).

Для отрицательных зарядов берется противоположное направление.

Сила Лоренца всегда направлена перпендикулярно скорости заряда и сообщает ему нормальное ускорение. Не изменяя модуля скорости, а лишь изменяя ее направление, сила Лоренца не совершает работы, и кинетическая энергия заряженной частицы при движении в магнитном поле не изменяется.

Если на движущийся электрический заряд помимо магнитного поля действует и электрическое поле напряженностью , то результирующая сила

- формула Лоренца.

1. Движение заряженной частицы вдоль силовой линии, (рис. 10).

,

магнитное поле не действует на частицу.

Заряженная частица движется по инерции равномерно прямолинейно.

2. Движение заряженной частицы перпендикулярно силовым линиям, (рис. 11).

Пусть в однородное магнитное поле с индукцией влетела заряженная частица массой m с зарядом q перпендикулярно магнитным силовым линиям со скоростью .

В каждой точке поля на частицу действует . Т.к. , то . Ускорение изменяет только направление скорости, , значит, . В этих условиях заряженная частица движется равномерно по окружности.

Согласно II закону Ньютона:

,

. (2)

Т.к. все величины, входящие в правую часть выражения (2), постоянны, радиус кривизны R меняться не будет. Постоянный радиус кривизны имеет только окружность. Следовательно, движение заряда в плоскости, перпендикулярной магнитному полю, будет происходить по окружности. Чем больше , тем меньше R.

Важным результатом является тот факт, что период обращения заряда в однородном магнитном поле не зависит от его скорости.

если . (3)

Частицы, имеющие бóльшую скорость, движутся по окружности бóльшего радиуса, однако время одного полного оборота будет таким же, что и для более медленных частиц, движущихся по окружности меньшего радиуса. Данный результат положен в основу действия циклических ускорителей элементарных частиц.

3. Движение заряженной частицы произвольно по отношению к линиям магнитной индукции (рис. 12). Вектор скорости можно разложить на 2 составляющие: .

В направлении сила Лоренца на заряд не действует, поэтому в этом направлении он движется равномерно прямолинейно с . В направлении, перпендикулярном , он движется по окружности со скоростью . Движение заряда представляет собой суперпозицию этих двух движений и происходит по винтовой линии, ось которой параллельна .

Радиус витка с учетом (2):

. (4)

Шаг винтовой линии (расстояние между соседними витками) с учетом (3):

.

Если движение происходит в неоднородном магнитном поле, индукция которого возрастает в направлении движения частицы (рис. 13), то R уменьшается с ростом согласно (4). На этом основана фокусировка пучка заряженных частиц в магнитном поле. Таким образом, с помощью неоднородного магнитного поля можно управлять пучками заряженных частиц, собирать их или рассеивать подобно тому, как управляют поведением пучков световых лучей с помощью оптических линз.

Рассмотренный принцип положен в основу действия электронных микроскопов.

Ускорители заряженных частиц - устройства, в которых создаются управляемые пучки высокоэнергетических заряженных частиц под действием электрических и магнитных полей.

Свойство независимости периода от скорости обращения используют для того, чтобы превратить траекторию ускоряемой частицы в спираль и уменьшить размеры ускорителя. Такой принцип положен в основу работы циклотрона - родоначальника целого семейства ускорителей с магнитным полем: синхротрона, синхрофазотрона и т.д.

Ускорительная камера циклотрона представляет собой вакуумную цилиндрическую коробку, помещенную между полюсами сильного электромагнита (рис. 14а). Камера состоит из двух металлических половинок - дуантов, в зазоре между которыми создается с помощью генератора переменное электрическое напряжение с амплитудой порядка (рис. 14б). Частицы вводятся внутрь камера с помощью специального впускного устройства.

При каждом пересечении зазора частица приобретает энергию . За оборотов ~10⁷эВ.

Бóльшая энергия в циклотроне не может быть достигнута из-за релятивистских эффектов. В этом случае применяют принцип автофазировки, предложеный советским физиком Векслером (1944 г.) и американским физиком Мак-Милланом (1945 г.).

В синхроциклотронах (фазотронах) медленно уменьшается частота подаваемого напряжения. В синхротронах меняется индукция магнитного поля . В синхрофазотронах - изменяется и . При этом возможно увеличение 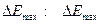~10⁹ - 10¹⁰ эВ.

Магнитные моменты электронов и атомов.

Опыт показывает, что все вещества являются магнетиками, т.е. способны под действием внешнего магнитного поля создавать собственное, внутреннее магнитное поле (приобретать собственный магнитный момент, намагничиваться).

Для объяснения намагничивания тел Ампер предположил, что в молекулах веществ циркулируют круговые молекулярные токи. Каждый такой микроток I_i имеет собственный магнитный момент и создает в окружающем пространстве магнитное поле (рис.1). В отсутствии внешнего поля молекулярные токи и связанные с ними ориентированы беспорядочно, поэтому результирующее поле внутри вещества и суммарный момент всего вещества равны нулю. При помещении вещества во внешнее магнитное поле магнитные моменты молекул приобретают преимущественно ориентацию в одном направлении, суммарный магнитный момент становится отличным от нуля, магнетик намагничивается. Магнитные поля отдельных молекулярных токов уже не компенсируют друг друга и внутри магнетика возникает его собственное внутреннее поле.

Рассмотрим причину этого явления с точки зрения строения атомов на основе планетарной модели атома. Согласно Резерфорду, в центре атома располагается положительно заряженное ядро, вокруг которого по стационарным орбитам вращаются отрицательно заряженные электроны. Электрон, движущийся по круговой орбите вокруг ядра, можно рассматривать как круговой ток (микроток). Поскольку за направление тока условно принято направление движения положительных зарядов, а заряд электрона отрицательный, направление микротока противоположно направлению движения электрона (рис.2).

Величину микротока I_e можно определить следующим образом. Если за время t электрон совершил N оборотов вокруг ядра, то через площадку, расположенную в любом месте на пути электрона, был перенесен заряд - заряд электрона).

Согласно определению силы тока,

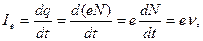
где частота вращения электрона.

Если ток I течет по замкнутому контуру, то такой контур обладает магнитным моментом, модуль которого равен

,

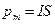где S - площадь, ограниченная контуром.

Для микротока такой площадью является площадь орбиты S = p r²

(r - радиус орбиты), а его магнитный момент равен

где w = 2pn - циклическая частота, - линейная скорость электрона.

Момент обусловлен движением электрона по орбите, поэтому называется орбитальным магнитным моментом электрона.

Магнитный момент p_m, которым обладает электрон вследствие своего движения по орбите, называется орбитальным магнитным моментом электрона.

Направление вектора образует с направлением микротока правовинтовую систему.

Как всякая материальная точка, движущаяся по окружности, электрон обладает моментом импульса:

.

Момент импульса L, которым обладает электрон вследствие своего движения по орбите, называется орбитальным механическим моментом. Он образует правовинтовую систему с направлением движения электрона. Как видно из рис.2, направления векторов и противоположны.

Оказалось, что, кроме орбитальных моментов (т.е. обусловленных движением по орбите), электрон обладает собственными механическим и магнитным моментами.

Первоначально существование и пытались объяснить, рассматривая электрон как шарик, вращающийся вокруг своей собственной оси, поэтому собственный механический момент импульса электрона получил название спин (от англ. spin - вращаться). В дальнейшем обнаружилось, что такое представление приводит к ряду противоречий и от гипотезы о «вращающемся» электроне отказались.

В настоящее время установлено, что спин электрона и связанный с ним собственный (спиновый) магнитный момент являются неотъемлемым свойством электрона, подобно его заряду и массе.

Магнитный момент электрона в атоме складывается из орбитального и спинового моментов:

Магнитный момент атома слагается из магнитных моментов входящих в его состав электронов (магнитным моментом ядра ввиду его малости пренебрегают):

.