Форма среднего индекса.

Сводный индекс может быть исчислен как средняя величина из индивидуальных индексов. Форма среднего индекса используется в тех случаях, когда в агрегатной форме индекс на основе имеющейся информации рассчитать невозможно. Однако форму средней для этого нужно выбрать таим образом, чтобы полученный средний индекс был бы тождественен исходному агрегатному индексу. В практике статистики в большинстве случаев принято все количественные индексы рассчитывать как средние арифметические, а все качественные как средние гармонические.

Выведем средний арифметический индекс из агрегатного в общем виде.

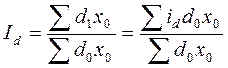, т.к. . Отсюда .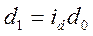

Аналогично записываются все конкретные количественные индексы:

Индекс физического объема продукции:

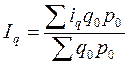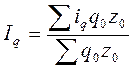или , или .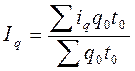

Индекс посевной площади: ;

Индекс численност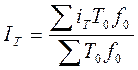и: или ;

Выведем средний гармонический индекс из агрегатного в общем виде.

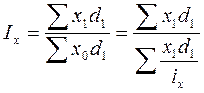, т.к. 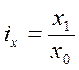. Отсюда .

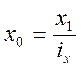Аналогично записываются все качественные индексы (кроме исключения).

Индекс цен: ;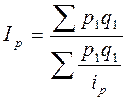

Индекс себестоимости: ;

Индекс урожайности: ;

Индекс заработной платы: ;

Индекс производительности труда по выработке: ;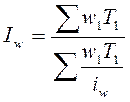

Исключение: индекс производительности труда по трудоемкости. 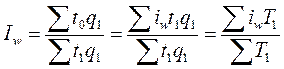, т.к. 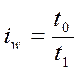. Отсюда .

Численные значения индексов производительности труда в обоих случаях будут одинаковыми. Изменение же явления в абсолютном выражении определяется, так же как и в агрегатной форме, разностью числителя и знаменателя индекса (исключение индекс производительности труда по трудоемкости ).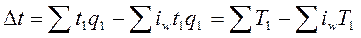

10.5.Базисные и цепные индексы.

При изучении динамики явления за ряд последовательных периодов (лет, месяцев т.д.) рассчитывают ряд индексов. Эти индексы показывают изменение явления либо по отношению к постоянной базе (базисные индексы), либо по отношению к переменной базе (цепные индексы). Цепные и базисные индексы могут быть индивидуальными и общими. Расчет индивидуальных индексов при этом прост. (Для удобства записи отсчет времени начнем с первого периода). Тогда качественные базисные индивидуальные индексы в общем виде 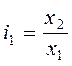; ; 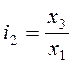; 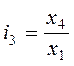и т.д.

Цепные: 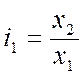; ; 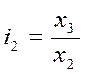; 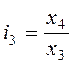и т.д.

Аналогично рассчитываются и количественные базисные и цепные индивидуальные индексы.

Взаимосвязь между ними: произведение цепных индексов равно базисному: .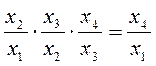

При построении базисных и цепных общих индексов возникает проблема весов. Веса при этом могут быть постоянными (т.е. одинаковыми во всех индексах) и могут быть переменными (т.е. изменяющимися от индекса к индексу).

В большинстве случаев принято все индексы (базисные и цепные) количественных показателей записывать с постоянными весами. В общем виде это выглядит так:

базисные индексы

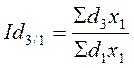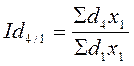; ; ; и т.д.

цепные индексы:

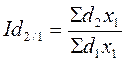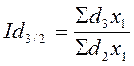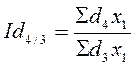; ; ; и т.д.

Взаимосвязь между ними в этом случае сохраняется: произведение цепных индексов равно базисному индексу: .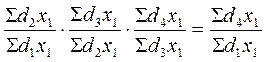

Базисные и цепные индексы качественных показателей в большинстве случаев записываются с переменными весами. В общем виде это будут:

базисные индексы:

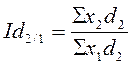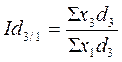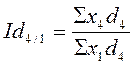; ; и т.д.

цепные индексы:

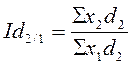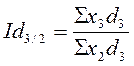; ; ; и т.д.

Между базисными и цепными индексами с переменными весами вышеуказанная взаимосвязь отсутствует.

( Формулы базисных и цепных индексов конкретных показателей смотри в Приложении 2).