Пример1

Движение точки М задается уравнениями:

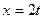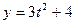см; см; .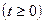

Определить кинематические элементы движения: траекторию, скорость и ускорение точки М. Указать момент времени, когда вектор скорости точки М образует с горизонтальной осью x-ов угол в 60⁰.

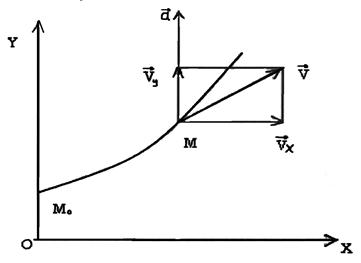
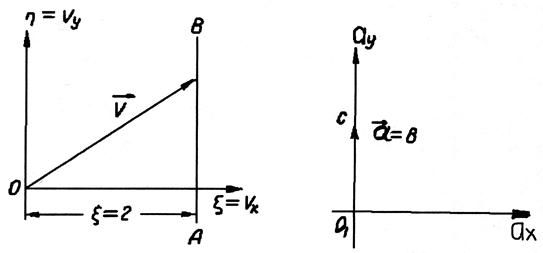
Построить годограф скоростей и ускорений.

Решение. Исключая из уравнений движения параметр t, найдем уравнение траектории: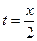

и

.

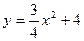Это есть уравнение параболы, симметричной относительно оси y-ов. Так как по условию 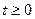, то 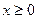и, следовательно, траекторией будет служить правая ветвь параболы. В начальный момент точка (t=0) находилась в вершине параболы (x=0, y=4).

Дифференцируя уравнения движения, найдем проекции скорости ускорения на координатные оси:

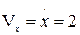см/сек; 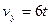см/сек.

Величина скорости равна:

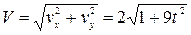см/сек.

Далее находим проекции ускорения на координатные ос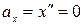и:

и 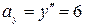см/сек².

Следовательно, ускорение в каждой точке траектории направлено по вертикали вверх и имеет постоянную величину, равную:

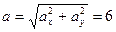см/сек².

Для того чтобы найти момент времени t=t₁, когда скорость точки М образует с осью х-ов угол в 60⁰, воспользуемся равенством:

.

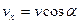Полагая здесь 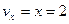, 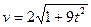и 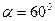, получим: ,

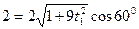Откуда следует: 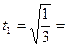0,57 сек.

Годографом скорости будет служить прямая АВ, параллельная оси 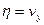с уравнением .

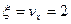Годографом ускорений будет служить точка С с координатами a_x=0 и a_y=6.