
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Если угол поворота измеряется в радианах, а время - в секундах, то единицей угловой скорости будет

В технике угловую скорость определяют числом оборотов в минуту, обозначая эту величину как n об/мин. Зависимость между угловой скоростью и числом оборотов в минуту определяется по формуле:
 1/cек.
1/cек.
Угловое ускорение характеризует изменение угловой скорости с течением времени.
|
Учтем, что 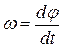 , тогда
, тогда  , или
, или  .
.
Единица измерения углового ускорения:
[ε] = 1/c2 = с-2 .
Вращение будет ускоренным, если угловая скорость и угловое ускорение будут иметь одинаковые знаки: ω > 0, ε > 0 или ω < 0, ε < 0.
Вращение будет замедленным, если: ω > 0, ε < 0 или ω < 0, ε > 0.
2. Скорости точек при вращательном движении
Все точки вращающегося твердого тела описывают окружности, плоскости которых перпендикулярны оси вращения, а центры лежат на этой оси.
В самом деле, в силу неизменяемости расстояний АМ и ВМ точка М должна постоянно оставаться как на поверхности сферы, описанной из точки А радиусом АМ, так и на поверхности сферы, описанной их точки В радиусом ВМ. Следовательно, точка М остается на линии пересечения обеих сфер, т.е. на окружности, плоскость которой перпендикулярна к АВ, центр лежит на этой прямой, а радиус равен расстоянию точки до оси вращения.
Положение точки М, находящейся на окружности радиуса h (рис. 1), в соответствии с естественным способом задания, определяется длиной дуги окружности, отсчитываемой от начального положения МО, находящегося на неподвижной плоскости:


Определяем скорость точки М

Скорость точки вращающегося твердого тела равна произведению угловой скорости тела на ее радиус вращения

Дата добавления: 2014-12-03; просмотров: 276; Мы поможем в написании вашей работы!; Нарушение авторских прав |
