Поступательное движение твердого тела. Поступательным называется такое движение твердого тела, при котором любая прямая, жестко связанная с телом

Поступательным называется такое движение твердого тела, при котором любая прямая, жестко связанная с телом, перемещается параллельно самой себе.

Основное свойство: при поступательном движении все точки тела движутся одинаково, т.е. описывают одинаковые траектории и имеют геометрически равные скорости и ускорения.

Поступательное движение характеризуется движением любой его точки, поэтому для определения кинематических характеристик поступательного движения достаточно определить соответствующие характеристики одной из его точек.

Пример. Точка А кривошипа движется со скоростью V_A = 0,8 м/с. ОА =0,4 м. Определить траекторию, скорость и ускорение точки М.

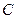
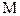
Решение. Движение треугольной пластины ABM, соединенной шарнирно с кривошипами ОА и СВ, является поступательным, поэтому его можно характеризовать движением точки А. Точка описывает окружность радиуса ОА, скорость точки направлена по касательной к этой окружности, т.е. перпендикулярно ОА.

Скорости всех точек пластины одинаковы и равны скорости точки А.

V_М = V_D = V_A.

Точка А движется с постоянной скоростью, поэтому она имеет нормальное ускорение, направленное по кривошипу к точке О.

Ускорения всех точек пластины одинаковы и равны ускорению точки А:

а_М = а_В = a_A.