КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Полученное равенство связывают углы поворота контактирующих тел.
Скорости точек, лежащих на соединенных ободах обоих тел для всех видов сцепления равны:
, 
.
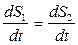Угловые скорости тел, находящихся в зацеплении, обратно пропорциональны их радиусам.
.
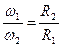4. Ускорения точек вращающегося тела.
Ускорение точки, движущейся по криволинейной окружности , раскладывается на нормальную и касательную составляющие:
.
Эти составляющие вычисляются по формулам, определяемым естественным способом задания:
Подставим в эти формулы значение скорости точки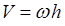 
, учитывая, что ρ = h, получим:
Окончательно касательное и нормальное ускорения определяются по формулам:
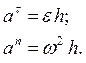
Касательное ускорение (рис.1) направлено перпендикулярно радиусу вращения и совпадает с вектором скорости, если вращение тела является ускоренным; касательное ускорение противоположно вектору скорости при замедленном вращении.
Нормальное ускорение всегда направлено по радиусу к центру вращения.
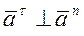
Модуль полного ускорения точки М (рис. 10):
.
Вектор полного ускорения образует с радиусом h угол μ, определяемый соотношением (рис.3):
В данный момент времени значения ε и ω для всех точек одинаковы, следовательно, угол μ также одинаков для всех точек, а модули ускорений точек пропорциональны радиусам вращения. Поле ускорений показано на рис. 11.
Пример:
Кривошип О1О2 вращается вокруг оси О1 с угловой скоростью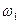 
. На палец О2 кривошипа свободно насажена шестерня радиуса r2 находящаяся в зацепление (зацепление внутреннее) с неподвижным колесом радиуса r3. Найти абсолютную угловую скорость Ω шестерни и её угловую скорость относительно кривошипа.
Решение. Колесо II участвуют в двух вращательных движениях: оно вращается с угловой скоростью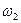 
относительно кривошипа O1O2 и вращается вместе с кривошипом относительно оси O1. В результате сложения этих двух вращений колесо II будет вращаться с угловой скоростью Ω относительно новой оси. Легко сообразить, что эта ось пройдет через точку С, где в данный момент соприкасается колесо II с неподвижным колесом III, так как скорость этой точки в данный момент равна нулю, и она является мгновенным центром скоростей для колеса II. Следовательно: 
.
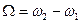Напишем скорость точки О2. Если рассматривать эту точку как принадлежащую кривошипу, то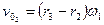 
,
если же эту точку рассматривать как принадлежащую колесу II, то 
.
Таким образом,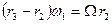 
.
Абсолютная угловая скорость вращения колеса II будет равна
.
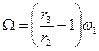Угловая скорость 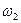колеса II относительно кривошипа О1О2 равна
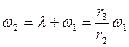
5*. Векторные формулы
Угловую скорость можно представить в виде вектора 
.
Вектор угловой скорости направлен по оси вращения в ту сторону, откуда вращение тела видно против часовой стрелки (рис.5), а его модуль равен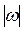 
.
Угловое ускорение тела также можно представить в виде вектора
.
Направление вектора углового ускорения совпадает с направлением вектора угловой скорости, если тело вращается ускоренно (рис.12), и эти векторы противоположны по направлению, если вращение тела – замедленное.
Вектор скорости точки вращающегося тела равен векторному произведению вектора угловой скорости тела на радиус – вектор, проведенный из любой точки, взятой на оси вращения, в данную точку.
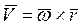
Дата добавления: 2014-12-03; просмотров: 146; Мы поможем в написании вашей работы!; Нарушение авторских прав |