КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Естественный способ задания движения точки
Этот способ применяется в том случае, когда траектория, по которой движется точка, известна. Выберем на траектории фиксированную точку О, (рис.1.2) и направление положительного отсчета дуги, тогда положение точки М в любой момент времени будет определяться значением дуговой координаты S=OM, отсчитываемой от точки О.
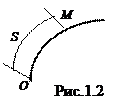Законом движения точки называется зависимость дуговой координаты от времени: 
.
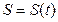Введем единичный вектор 
, направленный по касательной к траектории точки в сторону положительного отсчета расстояния s.
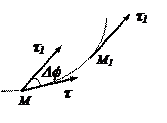Вектор скорости точки равен
где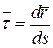 
и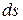 
– дифференциал дуги траектории точки.
Тогда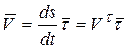 
, 
Проекция 
вектора скорости точки на касательную равна производной от дуговой координаты по времени.
Если > 0, то скорость точки направлена в сторону положительного отсчета дуговой координаты, если < 0, то скорость направлена в противоположную сторону.
Выразим ускорение точки через характеристики естественного способа задания. Простейшей полоской кривой является окружность
Через 3 точки можно провести плоскость и
окружность с центром (СММ1,М2). Предельное
положение плоскости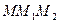 
, когда точки
и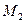 
стремятся к точке 
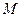, называется
соприкасающейся плоскостью.
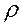
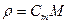- радиус кривизны траектории в точке M
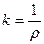- кривизна
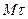- касательная oрm 
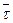направлен по
касательной в сторону возрастания
дуговой координаты
Mn-главная нормаль, opm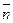 
направленной по нормале,
лежащей в соприкасающейся
плоскости в сторону
вогнутости траектории
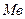-бинормаль, opm 
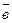перпендикулярно
соприкасающийся
плоскости в ту сторону
откуда кратчайшее совмещение
оси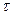 
c n видно происходящим
против хода часовой стрелки,
т.е. по правилу правого винта
Преобразуем выражение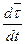 
, учитывая, что 
, 
.
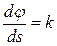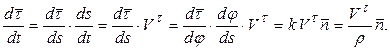
Тогда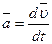 
примет вид
.
Вектор ускорения равен геометрической сумме векторов, один из которых 
направлен по касательной, а другой 
- по главной нормали.
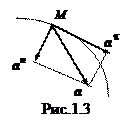Ускорение т очки М лежит в соприкасающейся плоскости
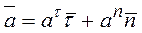
Касательное и нормальное ускорения определяются формулами:
| |
; 
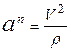
Величина 
может быть положительной, отрицательной и равной нулю.
Модуль полного ускорения: 
1. Есл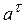и 
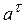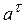и имеют одинаковые знаки ( > 0, > 0 или < 0, < 0), то движение точки будет ускоренным (рис.1.4, а).
2. Eсли 
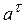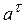и имеют разные знаки ( > 0, < 0 или < 0, > 0), то движение будет замедленным (рис.1.4, б).
3. Если 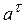= 0, криволинейное движение точки будет равномерным (рис.1.4, с ).
 |
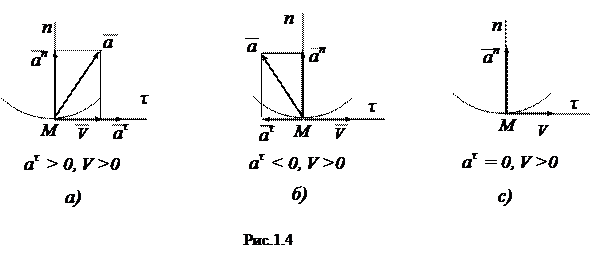Касательное ускорение характеризует изменение скорости по величине. Величина нормального ускорения всегда положительна, это означает, что вектор
направлен по главной нормали в сторону вогнутости кривой.
Нормальное ускорение меняет скорость по направлению.
При равномерном движении точки по криволинейной траектории касательное ускорение равно нулю, так как модуль скорости движения является постоянным.
При прямолинейном движении нормальное ускорение равно нулю, так как в этом случае 
.
Если движение точки является прямолинейным и равномерным, то и нормальное и касательное ускорения равны нулю.
При движении точки по окружности радиуса R нормальное ускорение равно 
.
Лекция №6
Дата добавления: 2014-12-03; просмотров: 201; Мы поможем в написании вашей работы!; Нарушение авторских прав |