
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Проблема ідентифікації.
При переході від зведеної форми моделі до структурної економетріст стикається з проблемою ідентифікації. Ідентифікація - це єдиність відповідності між наведеної та структурної формами моделі.
Структурна модель (3) у повному вигляді містить m(m+n-1) параметрів, а зведена форма моделі в повному вигляді містить mn параметрів. Тобто в повному вигляді ЗФМ містить більше число параметрів, ніж СФМ. Відповідно m(m+n-1) параметрів СФМ не можуть бути однозначно визначені з mn параметрів ЗФМ.
Щоб отримати єдино можливе рішення для структурної моделі, необхідно припустити, що деякі з структурних коефіцієнтів моделі через слабкий взаємозв'язок ознак з ендогенною змінною в лівій частини системи рівнянь дорівнюють 0. Тим самим зменшиться кількість структурних коефіцієнтів моделі.
З позиції ідентифікації структурні моделі можна підрозділити на три види:
а) ідентифіковані;
б) неідентифіковані;
в)понад ідентіфіковані.
Модель ідентифікована, якщо всі структурні її коефіцієнти визначаються однозначно, єдиним чином за коефіцієнтами ЗФМ, тобто число параметрів СФМ дорівнює числу параметрів ЗФМ. У цьому випадку структурні коефіцієнти моделі оцінюються через параметри ЗФМ і модель ідентифікується.
Модель неідентіфікована, якщо число зведених коефіцієнтів менше числа структурних коефіцієнтів, і в результаті структурні коефіцієнти не можуть бути оцінені через коефіцієнти зведеної форми моделі.
Модель понад ідентифікована, якщо число зведених коефіцієнтів більше числа структурних коефіцієнтів. У цьому випадку на основі коефіцієнтів зведеної форми можна отримати два і більше значень одного структурного коефіцієнта. У цій моделі число структурних коефіцієнтів менше числа коефіцієнтів зведеної форми. Понад ідентіфікована модель на відміну від неідентифікованої моделі практично вирішувана, але вимагає для цього спеціальних методів обчислення параметрів.
Структурна модель завжди являє собою систему спільних рівнянь, кожне з яких потрібно перевіряти на ідентифікацію. Модель вважається ідентифікованою, якщо кожне рівняння системи ідентифіковане. Якщо хоча б одне з рівнянь системи неідентифіковане, то і вся модель вважається неідентифікованою.
Понад ідентіфікована модель має хоча б одне понад ідентіфіковане рівняння.
Якщо позначити число ендогенних змінних у i-му рівнянні системи через Н, а число екзогенних (зумлених) змінних, які містяться в системі, але не входять в дане рівняння, - через D, то умова ідентифікації моделі може бути записана у вигляді рахункового правила:
Таблиця 1.
| D+1=H | Рівняння ідентіфіковане |
| D+1<H | Рівняння неідентіфіковане |
| D+1>H | Рівняння понад ідентіфіковане |
Для оцінки параметрів структурної моделі система повинна бути ідентифікована або понад ідентифікована.
Розглянуте рахункове правило відображає необхідну умову але не достатню умову ідентифікації. Рівняння є ідентифікованим, якщо щодо відсутніх у ньому змінним (ендогенним і екзогенним) можна з інших рівнянь системи отримати матрицю, визначник якої не дорівнює нулю, а ранг матриці не менше, ніж число ендогенних змінних у системі без одного.
У економетричних моделях часто поряд з рівняннями, параметри яких повинні бути статистично оцінені, використовуються балансові тотожності змінних, коефіцієнти яких дорівнюють ±1. У цьому випадку, хоча саме тотожність і не вимагає перевірити на ідентифікацію, бо коефіцієнти при змінних в тотожності відомі, у перевірці на ідентифікацію власне структурних рівнянь системи тотожності беруть участь.
Приклад 1.Розглянемо систему одночасних рівнянь:

 (7)
(7)
Составимо таблицю 2 для перевірки рахункового правила.
Таблиця 2.
| Рівняння | Число присутніх у рівнянні ендогенних змінних Н | Число відсутніх у рівнянні екзогенних змінних D | Рахункове правило |
| I | y1,y2,y3, H=3 | x3,x4, D=2 | H=D+1, рівняння ідентіфіціруємо |
| II | y1,y2, H=2 | x4, D=1 | H=D+1, рівняння ідентіфіціруємо |
| III | y1,y2,y3, H=3 | x1,x2, D=2 | H=D+1, рівняння ідентіфіціруємо |
Таким чином, система (7) ідентіфіціруємо.
Нехай у розглянутій системі (7) a21=0, a33=0. Тоді система прийме вигляд:
 (8)
(8)
Побудуємо таблицю 3 для перевірки рахункового правила.
Таблиця 3.
| Рівняння | Число присутніх у рівнянні ендогенних змінних Н | Число відсутніх у рівнянні екзогенних змінних D | Рахункове правило |
| I | y1,y2,y3, H=3 | x3,x4, D=2 | H=D+1, рівняння ідентіфіціруємо |
| II | y1,y2, H=2 | x1, x4, D=2 | H<D+1, рівняння понад ідентіфіціруємо |
| III | y1,y2,y3, H=3 | x1,x2, x3, D=3 | H<D+1, рівняння понад ідентіфіціруємо |
Модель (8) в цілому понад ідентіфіціруємо.
Нехай в останньому рівнянні системи (8) останнє рівняння має вигляд:
y3=b31y1+b32y2+a31x1+a32x2+a34x4,
тобто в останне рівняння включено ще дві екзогенні змінні х1,х2. В цьому випадку рівняння стає не індентіфікованим, так як Н=3, D=1 та (D+1<Н, 1+1<3).
І так, не дивлячись на те що перше рівняння ідентіфіковане, друге понад ідентіфіковане, вся модель вважається неідентифікованою і не має статистичного рішення.
Доцільність перевірки умови ідентифікації моделі через визначник матриці коефіцієнтів, відсутніх у даному рівнянні, але присутніх в інших рівняннях, пояснюється тим, що можлива ситуація, коли для кожного рівняння системи виконано рахункове правило, а визначник матриці названих коефіцієнтів дорівнює нулю. У цьому випадку дотримується лише необхідне, але не достатня умова ідентифікації.
Приклад 2.Розглянемо систему одночасних рівнянь:

 (9)
(9)
Перевіремо кожне рівняння системи (9) на необхіне та достатнью умови ідентіфікації. Составимо таблицю 4 для перевірки рахункового правила.
Таблиця 4.
| Рівняння | Число присутніх у рівнянні ендогенних змінних Н | Число відсутніх у рівнянні екзогенних змінних D | Рахункове правило |
| I | y1,y2,y3, H=3 | x3,x4, D=2 | H=D+1, рівняння ідентіфіковане |
| II | y1,y2, H=2 | x1, D=1 | H=D+1, рівняння ідентіфіковане |
| III | y1,y2,y3, H=3 | x3, x4, D=2 | H=D+1, рівняння ідентіфіковане |
Необхідна умова ідентифікації виконана.
Для перевірки на достатню умову ідентифікації першого рівняння заповнимо таблицю 5,
Таблиця 5.
| Рівняння | Змінні | А= 
|
| х3 | х4 | |
| а23 | а24 | |
Достатня умова ідентифікації для першого рівняння не виканане.
Для перевірки на достатню умову ідентифікації другого рівняння заповнимо таблицю 6.
Таблиця 6.
| Рівняння | Змінні | А= 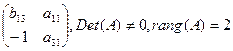
|
| у3 | х1 | |
| b13 | а11 | |
| -1 | a31 |
Достатня умова ідентифікації для другого рівняння виканане.
Для перевірки на достатню умову ідентифікації третього рівняння заповнимо таблицю 7.
Таблиця 7.
| Рівняння | Змінні | А= 
|
| х3 | Х4 | |
| а23 | a24 |
Достатня умова ідентифікації для третього рівняння не виканане.
Висновок: в цілому структурна модель не може бути ідентіфікованою.
Дата добавления: 2014-12-03; просмотров: 385; Мы поможем в написании вашей работы!; Нарушение авторских прав |