Метод максимальної правдоподібності з повною інформацією та метод максимальної правдоподібності при обмеженій інформації.

Метод максимальної правдоподібності розглядається як найбільш загальний метод оцінювання, результати якого при нормальному розподілу ознак збігається з МНК. Однак при великому числі рівнянь системи цей метод призводить до досить складних обчислювальних процедур. Тому в якості модифікації використовується метод максимальної правдоподібності при обмеженій інформації (метод найменшого дисперсійного відношення), розроблений у 1949 р. Т. Андерсоном і Н. Рубіним.

На відміну від методу максимальної правдоподібності в даному методі зняті обмеження на параметри, пов'язані з функціонуванням системи в цілому. Це робить рішення більш простим, але трудомісткість обчислення залишається досить високою. Незважаючи на його популярність, до середини 60-х років він був витіснений ДМНК у зв'язку з набагато більшою простотою останнього.

Подальшим розвитком ДМНК є ТМНК, запропонований в 1962 р. А. Зельнером та Г. Тейлом. Цей метод оцінювання придатний для всіх видів рівнянь структурної моделі. Однак при деяких обмеженнях на параметри більш ефективним є ДМНК.

Приклад 3.Розглянемо застосування НМНК для найпростішої ідентифікованої моделі з двома ендогенними і двома екзогенними змінними:

Для побудови даної моделі ми маємо в своєму розпорядженні деякою інформацією з п'яти регіонів:

ПФМ має вигляд:

де u₁,u₂ - випадкові похибки ЗФМ.

Для кожного рівняння ЗФМ використовуємо МНК та визначаємо δ коефіцієнти.

Щоб спростити процедуру розрахунків будемо працювати з відхиленнями від середніх, тобто з τ= , .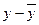

Тоді для першого рівняння ЗФМ система нормальних рівнянь має вигляд:

Стосовно до нашого прикладу маємо:

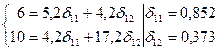
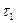=0,852t₁+0,373t₂+u₁

Для другого рівняння ЗФМ система нормальних рівнянь має вигляд:

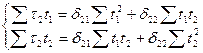
Стосовно до нашого прикладу маємо:

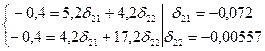
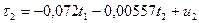
Таким чином, ЗФМ має вигляд:

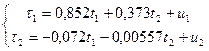
Перейдемо від ЗФМ до СФМ:

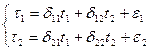
Для цієї мети з першого рівняння ЗФМ треба виключити t₂ виключивши його з другого рівняння ЗФМ і підставивши в перше:

t₂=(-0,072 t₁-τ₂)/0,00557.

Тоді 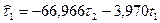- перше рівняння СФМ.

Щоб знайти друге рівняння СФМ треба з другого рівняння виключити t₁ і підставити в друге рівняння:

t₁=(-0,373 t₂-τ₁)/0,852.

Тоді 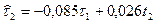- друге рівняння СФМ.

І так, структурна форма моделі має вигляд:

Перейдемо від середніх значень до змінних х та у. Вільні члени рівнянь знайдемо за формулами:

A₀₁=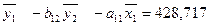

A₀₂=

Тоді структурна форма моделі прийме вигляд:

Питання для самоконтролю.

1. Запишіть в загальному вигляді структурну форму моделі на основі одночасових рівнянь.

2. Що означає зведена форма моделі? Як її одержати?

3. Дайте визначення рекурсивних систем і запишіть модель на основі рекурсивної системи.

4. Яка система рівнянь називається точно ідентифікованою?

5. Яка система рівнянь називається надідентифікованою?

6. Запишіть умову ідентифікованності системи рівнянь.

7. На основі якого методу можна оцінити параметри моделі, якщо вона складається із системи рекурсивних рівнянь?

8. Який метод оцінки параметрів можна застосувати, коли всі рівняння моделі є точно ідентифікованими?

9. На основі якого методу можна оцінити параметри моделі, якщо вона має надідентифіковані рівняння?

10. Чи можна виконувати оцінку параметрів моделі окремо для групи точно ідентифікованих і надідентифікованих рівнянь?