Структурна та приведена форма моделі.

При використанні окремих рівнянь регресії, наприклад для економічних розрахунків, в більшості випадків припускають, що аргументи (фактори) можна зміняти незалежно один від іншого. Однак це припущення є дуже грубим: практично зміна однієї змінної, як правило, не може відбуватися при абсолютній незмінності інших. Її зміна проїзведе до зміни во всій системі взаємо зв’язаних при знаків. Це означає що, окреме рівняння регресії не може характеризувати істинні зміни окремих при знаків на варіацію результативної змінної.

Саме тому в останні десятиліття в економічних дослідженнях важливе місце зайняла проблема опису структури зв'язків між змінними системою так званих одночасних рівнянь, званих також структурними рівняннями. Саме тому в останні десятиліття в економічних дослідженнях важливе місце зайняла проблема опису структури зв'язків між змінними системою так званих одночасних рівнянь, званих також структурними рівняннями.

Система рівнянь в економетричних дослідженнях може бути побудована по-різному.

Можлива система незалежних рівнянь, коли кожна залежна змінна у розглядається як функція одного і того ж набору факторів х:

(1)

Набір факторів у кожному рівнянні може варіроватися. Кожне рівняння системи незалежних рівнянь може розглядатися самостійно. Для знаходження його параметрів використовують метод найменших квадратів (МНК). По суті, кожне рівняння цієї системи є рівнянням регресії. Так як фактичні значення залежної змінної відрізняються від теоретичних на величину випадкової похибки, то в кожному рівнянні присутня випадкова похибка ε_i.

Якщо залежна змінна у одного рівняння виступає у вигляді фактора х в другому рівнянні, то дослідник може будувати модель у вигляді системи рекурсійних рівнянь:

(2)

У даній системі залежна змінна y включена в кожне наступне рівняння в якості факторів усі залежні змінні попередніх рівнянь поряд з набором власне факторів х. Кожне рівняння цієї системи може розглядатися самостійно, та його параметри можна знайти методом найменших квадратів.

Найбільш розповсюджене в економетричних дослідженнях знайшла система взаємо залежних рівнянь:

(3)
Система взаємно залежних рівнянь получила назву системи одночасових структурних рівнянь. Тим самим підкреслюється, що в системі одні і тіж змінні одноразово розглядаються як залежні в одних рівняннях, так і як незалежні в інших. В економетриці ця система рівнянь получила назву структурної форми моделі (СФМ).
На відміну від попередніх систем кожне рівняння системи одночасних рівнянь не може розглядатися самостійно, і для знаходження його параметрів традиційний метод МНК непридатний. З цією метою використовуються спеціальні прийоми оцінювання.

Система спільних, одночасних рівнянь (СФМ) зазвичай містить ендогенні та екзогенні змінні.
Ендогенні змінні - це залежні змінні, число яких дорівнює числу рівнянь в системі і які позначаються через у.
Екзогенні змінні - це зумовлені змінні, що впливають на ендогенні змінні (незалежні) і які позначаються через х.

Економічні змінні можуть виступати в одних моделях як ендогенні, а в інших як екзогенні змінні.

Структрная форма моделі в правій частині містить при ендогенних змінних коефіцієнти b_ik і екзогенних змінних - коефіцієнти a_ij, які називаються структурними коефіцієнтами моделі. Всі змінні в моделі виражені у відхиленнях від середнього рівня, тобто під х мається на увазі ( ), а під у - відповідно ( ). Тому вільний член у кожному рівнянні системи (3) відсутній.

Використання МНК для оцінювання структурних коефіцієнтів моделі дає, як прийнято вважати в теорії, зміщені і неспроможні оцінки. Тому зазвичай для визначення структурних коефіцієнтів моделі СФМ перетвориться в зведену форму моделі (ЗФМ).
Зведена форма моделі являє собою систему лінійних рівнянь ендогенних змінних від екзогенних:

(4)

де - коефіцієнти ЗФМ, u_i – залишкова величина для ЗФМ.

За своїм виглядом наведена форма моделі нічим не відрізняється від системи незалежних рівнянь, параметри якої оцінюються традиційним МНК. Застосовуючи МНК, можна оцінити , а потім оцінити значення ендогенних змінних через екзогенні.
Коефіцієнти ЗФМ представляють собою нелінійні функції коефіцієнтів СФМ. Розглянемо це положення на прикладі найпростішої структурної моделі.

Для структурної моделі вигляду

(5)

зведена форма моделі має вигляд

(6)

З першого рівняння (5) можна визначити у₂ слідуючим чином (заради спрощення виразу випадкову змінну опустимо):

y₂= .

Підставимо в друге рівняння (5) у₂:

або

y₁= .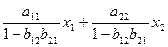

Поступивши з другим рівнянням системи (5) відповідно, получемо:

y₂= ,

тобто система (5) прийме вигляд:

Таким чином, можна зробити висновок про те, що коефіцієнти зведеної форми моделі будуть виражатися через коефіцієнти структурної форми наступним чином:

Слід зазначити, що ПФМ хоча і дозволяє отримати значення ендогенної змінної через значення екзогенної змінних, але аналітично вона поступається СФМ, тому що в ній відсутні оцінки взаємозв'язку між ендогенними змінними.