КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Расчет среднеквадратического отклонения
Среднее квадратическое отклонение характеризует среднее отклонение всех вариант вариационного ряда от средней арифметической величины.
Существует три способа расчета среднего квадратического отклонения: среднеарифметический, способом моментов и по амплитуде.
Возвратимся к нашему примеру.
1) При среднеарифметическом способе расчета применяется формула:
|
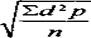
s =
d — отклонение отдельных вариант от средней арифметической (V-M)
р — частота
n — число наблюдений (при числе наблюдений менее 30, в знаменатель необходимо взять n—1).
Порядок вычисления среднего квадратического отклонения представлен в таблице
| Частота пульса V | Р | d (V - М) М = 72,3 | d2 | d2p |
| -12,3 | 151,29 | 151,29 | ||
| -10,3 | 106,09 | 212,18 | ||
| -8,3 | 68,89 | 206,67 | ||
| -6,3 | 39,69 | 119,07 | ||
| -4,3 | 18,49 | 55,47 | ||
| -2,3 | 5,29 | 47,61 | ||
| -0,3 | 0,09 | 0,54 | ||
| 1,7 | 2,89 | 20,23 | ||
| 3,7 | 13,69 | 150,59 | ||
| 5,7 | 32,49 | 162,45 | ||
| 7,7 | 59,29 | 237,16 |
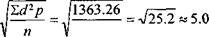n=54 ∑ 1363,26
s =
Среднее квадратическое отклонение, также как и среднюю арифметическую, можно рассчитать более простым способом, а именно способом моментов по формуле:
| s = √ | ∑d2p | - | ∑(dp)2 | |
| n | n2 |
где d - отклонение каждой варианты от условной средней (V-A).
Порядок вычисления среднего квадратического отклонения представлен в таблице (за условную среднюю принимаем М0 = 76 ударам в минуту).
| Частота пульса V | D(V-A) А=76 | d | dp | d2 | d2p |
| -16 | -16 | ||||
| -14 | -28 | ||||
| -12 | -36 | ||||
| -10 | -30 | ||||
| -8 | -24 | ||||
| -6 | -54 | ||||
| -4 | -24 | ||||
| -2 | -14 | ||||
| N = 54 ∑ = -200 ∑ = 2104 |
| s = √ | ∑d2p | - | ∑d2p2 | = √ | - | -2002 | = √25,2 | ≈ 5,0 | |
| n | n2 | 542 |
Результаты вычисления среднего квадратического отклонения среднеарифметическим способом и способом моментов идентичны. Однако, как указывалось выше, второй способ значительно убыстряет и упрощает расчеты. Если отсутствуют необходимые исходные данные для вычисления среднего квадратического отклонения обычным путем, может быть использован приближенный способ вычисления среднего квадратического отклонения по амплитуде вариационного ряда.
Среднее квадратическое отклонение, вычисленное по амплитуде, несколько отличается по величине от о, вычисленной обычными способами. Различие это тем больше, чем больше число наблюдений, использованных для составления вариационного ряда. Поэтому определение среднего квадратического отклонения по амплитуде более целесообразно производить преимущественно при ориентировочных расчетах.
Вычисление производится по формуле:
| s = | Am | = | Vmax-Vmin |
| k | k |
Am — амплитуда
k — коэффициент, соответствующий числу наблюдений (определяется по специальной таблице, в нашем примере при n=54 коэффициент равен 4,56)
| s = | 80-60 | = | ≈ 4,4 | |
| 4,56 | 4,56 |
Значения и для вычисления среднего квадратического отклонения (s) по амплитуде
| N | ||||||||||
| - | - | 1,13 | 1,69 | 2,06 | 2,33 | 2,53 | 2,70 | 2,85 | 2,97 | |
| 3,08 | 3,17 | 3,26 | 3,34 | 3,41 | 3,47 | 3,53 | 3,59 | 3,64 | 3.69 | |
| 3,73 | 3,78 | 3,82 | 3,86 | 3,90 | 3,93 | 3,96 | 4,00 | 4,03 | 4,06 | |
| 4,09 | 4,11 | 4,14 | 4,16 | 4,19 | 4,21 | 4,24 | 4,26 | 4,28 | 4,30 | |
| 4,32 | 4,34 | 4,36 | 4,38 | 4,40 | 4,42 | 4,43 | 4,45 | 4,47 | 4,48 4,48 | |
| 4,50 | 4,51 | 4,53 | 4,54 | 4,56 | 4,57 | 4,59 | 4,60 | 4,61 | 4,63 | |
| 4,64 | 4,65 | 4,66 | 4,68 | 4,69 | 4.70 | 4,71 | 4,72 | 4,73 | 4,74 | |
| 4,75 | 4,77 | 4,78 | 4,79 1 | 4,80П | 4,81 | 4,82 | 4,83 | 4,83 | 4,84 | |
| 4,85 | 4,86 | 4,87 | 4,88 | 4,89 | 4,90 | 4,91 | 4,91 | 4,92 | 4,93 | |
| 4,94 | 4,95 | 4,96 | 4,96 | 4,97 | 4,98 | 4,99 | 4,99 | 5,00 | 5,01 | |
| N | ||||||||||
| К | 5,02 | 5,49 | 5,76 | 5,94 | 6,07 | 6,18 | 6,28 | 6,35 | 6,42 | 6,48 |
Среднее квадратическое отклонение вычисленное обычными способами дает точную величину (s = 5,0). Однако различие это не слишком велико и, если бы были известны только крайние варианты ряда, приближенное вычисление среднего квадратического отклонения по амплитуде вариационного ряда имело бы смысл.
Итак, нахождение среднего квадратического отклонения позволяет судить о характере однородности исследуемой группы наблюдений. Если величина среднего квадратического отклонения небольшая, то это свидетельствует о достаточно высокой однородности изучаемого явления.
Среднюю арифметическую в таком случае следует признать вполне характерной, типичной для данного вариационного ряда. При очень большой величине сигмы средняя арифметическая в меньшей степени характеризует весь вариационный ряд, что говорит о значительной вариабельности изучаемого признака или явления или о неоднородности исследуемой группы.
Дата добавления: 2014-12-23; просмотров: 276; Мы поможем в написании вашей работы!; Нарушение авторских прав |