
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Таким образом, можно получить связь любой термодинамической функции состояния с изменением параметров состояния.
Неидеальный вклад.
Изменение любой термодинамической функции  при
при

|
Переходе системы к другим параметрам состояния могут быть определены с помощью соотношений в интегральной форме

|
(8.10) (8.11)

|

|
Необходимо знание уравнения состояния ψ(P,V,T) = 0, тогда интегралы (8.10) и (8.11) можно вычислить. Если за параметры V1 и
Р1 выбрать объём и давление, при которых 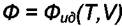 , то
, то
указанные интегралы дают возможность вычислить Фвз, т.е. вклад в величину термодинамической функции, обусловленный межмолекулярным взаимодействием.
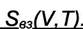
|
| В качестве примера вычислим |
Легко получить формулу аналогичную (8.8) для зависимости энтропии от объёма

|
Тогда

|
Но при изменении объёма идеального газа его энтропия изменится. Эту величину надо учесть при расчёте вклада в энтропию только от межмолекулярного взаимодействия. Рассчитаем вклад при изменении объёма для идеального газа
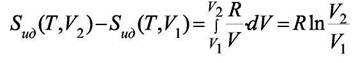
|

|
При V1 → ∞ S(T,V1) → Sид(Т,V1) и тогда, опустив индекс при V2 запишем
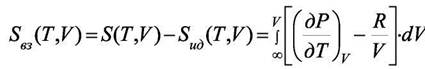
|
Для газа Ван-дер-Ваальса 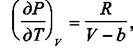 и тогда имеем
и тогда имеем
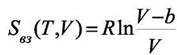
|
(8.12)
Рассчитаем  __ для газа
__ для газа  при переходе от состояния Р1 = 1 атм, Т = 373 К к состоянию
при переходе от состояния Р1 = 1 атм, Т = 373 К к состоянию  = 1000 атм и Т = 373 К.
= 1000 атм и Т = 373 К.
Из справочных данных для СО2: Ткр = 304 К, Ркр = 73 атм вычислим константы Ван-дер-Ваальса:
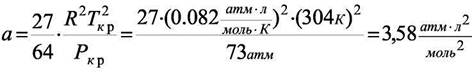

Значение объёма, удовлетворяющее уравнению Ван-дер-Ваальса при Р2 = 1000 атм и Т = 373 К находится из кубического уравнения (8.5) относительно V. Оно равно V= 0,0573 л/моль, тогда
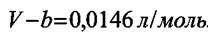 »
»
| Разность энтропии идеального газа при 1 атм и 1000 атм равна |
Подстановкой этих значений в уравнение (8.12) получим:
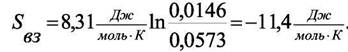
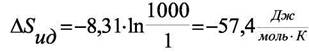
Общее изменение энтропии при переходе от 1 атм к 1000 атм составит − 68,8 ДжЯмольК).
Такой же расчёт можно провести и для энтальпии образования 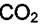 . Задача ставится таким образом: как изменится энтальпия образования
. Задача ставится таким образом: как изменится энтальпия образования 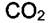 при переходе от стандартных условий к давлению 1000 атм. Температура системы постоянна и равна 373 К, что выше критической температуры. Значения энтальпии образования и
при переходе от стандартных условий к давлению 1000 атм. Температура системы постоянна и равна 373 К, что выше критической температуры. Значения энтальпии образования и
энтропии  в стандартных условиях равны
в стандартных условиях равны  = − 394
= − 394
кДж/моль, 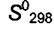 =213 Дж/мольК Результаты расчёта изменения
=213 Дж/мольК Результаты расчёта изменения
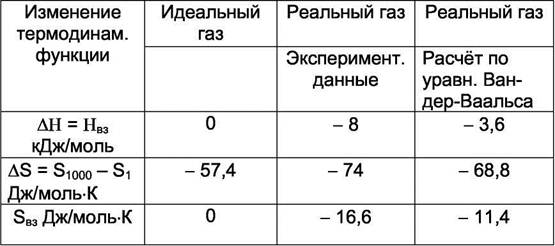
энтальпии образования и энтропии при переходе от Р = 1 атм к давлению Р = 1000 атм и Т = 373 К представлены в таблице 8.1.
Таблица 8.1. Изменения энтальпии образования и энтропии при переходе от Р = 1 атм к давлению Р = 1000 атм при Т = 373 К
Если уравнение Ван-дер-Ваальса представить в приведённых координатах 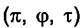 , то можно построить обобщённые диаграммы
, то можно построить обобщённые диаграммы
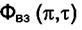 , справедливые для всех веществ, подчиняющихся этому уравнению.
, справедливые для всех веществ, подчиняющихся этому уравнению.
Дата добавления: 2014-12-23; просмотров: 231; Мы поможем в написании вашей работы!; Нарушение авторских прав |