КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Глава 1. теоретические основы построения индексной системы
Индексный метод используется широко в практике статистической работы наряду с вычислением относительных величин динамики, величин сравнения, систем выполнения плана и прочих характеристик. Во многих экономических расчетах он является наиболее распространенным статистическим показателем, используемым для обобщения характеристик и их изменения.
1.1. Понятие индекса и значение индексного
метода в статистическом анализе
Слово «индекс» (Index- лат.) означает указатель, показатель.
В статистикеиндексом является относительная величина, показывающая, во сколько раз уровень изучаемого явления в данных условиях отличается от аналогичного уровня в других условиях.
Различия условий могут проявляться во времени — строятся индексы динамики, в пространстве — территориальные индексы. Если условия анализа представлены в виде разных баз сравнения каких-либо условных уровней, например уровня договорных обязательств или планового задания, то рассматриваются индекс выполнения договорных обязательств или выполнения плана и т.п. Если плановый уровень сравнивается с фактическим уровнем предыдущего периода, то получают индекс планового задания.
Таким образом, при помощи индексов:
· Определяются средние изменения сложных, непосредственно несоизмеримых совокупностей во времени.
· Оценивается средняя степень выполнения плана по совокупности в целом или её части.
· Устанавливаются средние соотношения сложных явлений в пространстве.
· Определяется роль отдельных факторов в общем изменении сложных явлений во времени или пространстве.
В индексной теории существуют два направления: обобщающее (синтетическое) и аналитическое.
В обобщающем направлении индекс – это показатель среднего изменения уровня изучаемого показателя. В аналитической теории индексы – это показатели изменения уровня результативной величины под влиянием изменения индексируемой величины.
Например, величина индекса цен продукции, равная 1,1536, может быть истолкована в обобщающем значении как величина, указывающая на то, что цены на продукцию возросли в целом на 15,36 %, или в 1,1536 раза, а в аналитическом значении как показатель того, что в связи с изменением цен стоимость продукции (или размер выручки) увеличилась на 15,36 %.
С помощью индексных показателей решаются следующие основные задачи:
1) характеристика общего изменения сложного экономического показателя или формирующих его отдельных показателей-факторов;
например, затрат на производство продукции, стоимости произведенной продукции и т. д.)
2) определение влияния отдельных факторов на изменение динамики сложного явления;
например, увеличение выручки от реализации продукции, связанное с ростом цен или выпуска продукции в натуральном выражении).
3) обособление влияния изменения структуры явления на индексируемую величину.
Например, при изучении динамики среднеотраслевой себестоимости продукции исследуется влияние изменений в распределении объемов продукции по предприятиям отрасли).
Способы построения индексов зависят от содержания изучаемых показателей, методологии расчета исходных статистических показателей, имеющихся в распоряжении исследователя статистических данных и целей исследования.
По степени охвата элементов совокупности различают индивидуальные и сводные (общие) индексы [5, с. 340]
Индивидуальными называются индексы, характеризующие изменение только одного элемента совокупности.
Например, изменение объёма выпуска легковых автомобилей определенной марки за два периода.
Индивидуальный индекс обозначается буквой i.
Сводный индекс отражает изменение по всей совокупности элементов сложного явления. Если индексы охватывают не все элементы сложного явления, а лишь часть, то их называют групповыми (или субиндексами).
Например, сводный индекс характеризует динамику объема промышленной продукции. К субиндексам в этом случае могут быть отнесены индексы продукции по отдельным отраслям промышленности.
Сводный (общий) индекс обозначают буквой I.
В зависимости от содержания и характера индексируемой величины различают индексы количественных (объемных) показателей
(например, индекс физического объема продукции)
и индексы качественных показателей
(например, индексы цен, себестоимости).
При вычислении индексов различают сравниваемый уровень и уровень, с которым производится сравнение, называемый базисным. Выбор базы сравнения определяется целью исследования.
Возможны два способа расчета индексов – цепной и базисный. Цепные индексы получают путем сопоставления текущих уровней с предшествующим.В этом случае база сравнения меняется. Базисные индексы получают путем сопоставления текущего уровня с уровнем периода, принятого за базу сравнения, обычно январским.
При территориальных сравнениях за базу принимают данные по какой-либо одной части территории или итоговый показатель по всей изучаемой территории в целом.
При использовании индексов как показателей выполнения плана за базу сравнения принимаются плановые показатели.
В зависимости от методологии расчета различают агрегатные индексы и средние из индивидуальных индексов. Последние делятся на средние арифметические и средние гармонические индексы.
Агрегатные индексы качественных показателей могут быть рассчитаны как индексы переменного состава и индексы фиксированного (постоянного) состава. В индексах переменного состава сопоставляются показатели, рассчитанные на базе изменяющихся структур явлений, а в индексах фиксированного состава – на базе неизменной структуры явлений [5, с. 341-342].
Перечисленные идексы во всём своём многообразии образуют индексную систему.
На рис. 1. приведена структурная схема формирования индексных показателей.
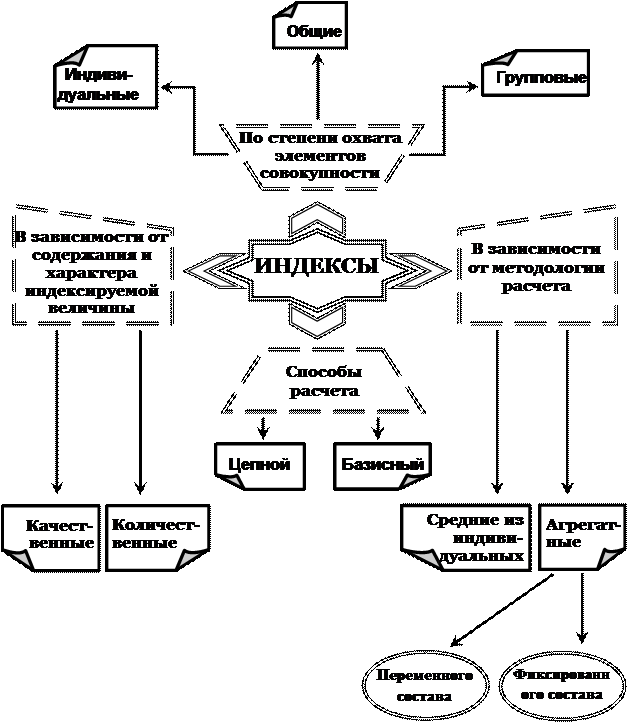
Рис. 1.Система индексов в статистике
1.2. построение индивидуальных индексов
Индивидуальные индексы дают возможность сравнивать в виде отношений отдельные признаки, их суммы или элементы. Чаще всего сравниваются числовые значения цен, объёмы и себестоимости продукции, другие показатели за разные периоды времени или по разным территориальным признакам.
С учётом степени охвата элементов изучаемой совокупности индивидуальный индекс является наиболее простым в индексной системе. От обычных относительных величин индексы отличает то, что они предназначены для описания характеристик отношений сложных явлений, складывающихся под влиянием различных причин.
Индексы выявляют роль и значение отдельных условий и составных частей сложных явлений. Они применяются также для изучения роли факторов, оказывающих влияние на изменение исследуемого явления. Так, с помощью взаимосвязи индексов можно определить, в какой мере увеличение производительности труда влияет на рост объёма продукции и какое влияние на этот показатель оказывает увеличение численности производственного и непроизводственного персонала.
Индивидуальный индекс - это относительный показатель, выражающий изменение одного отдельного элемента сложного экономического явления или соотношение отдельных элементов совокупности.
Вычисление индивидуальных индексов обозначаемых буквой “i” не вызывает затруднений. В числителе индивидуального индекса - величина индексируемой величины в текущем периоде, а в знаменателе - в базисном периоде.
В общем виде индивидуальный индекс – это обычный относительный показатель:
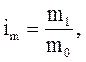 (1)
(1)
где m1, m0 – значения величины в текущем и базисном периоде.
Для удобства в теории статистики разработана определенная символика, в том числе для индексируемых величин при построении индивидуальных индексов. Так, количество единиц данного вида продукции (товаров) обозначается “q”, цена единицы продукции (товаров) - “p”, себестоимость единицы продукции - “z”, трудоемкость единицы изделия - “t” и т.д.
Чаще всего используются индивидуальные индексы, характеризующие изменение количества произведенной продукции одного вида, соотношение цен одного товара, трудоемкости одного изделия и т.д.
Индивидуальный индекс себестоимости характеризует изменение уровня себестоимости единицы какого-либо вида продукции в отчетном периоде по сравнению с базисным и вычисляется по формуле:
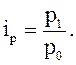 (2)
(2)
Например. Определяется индивидуальный индекс себестоимости продукции во втором квартале N года по сравнению с первым кварталом N года. Его значение равно отношению себестоимости продукции во втором квартале - 350 тыс. рублей к себестоимости продукции в первом квартале - 310 тыс. рублей.
iz = z1 : z0 = 350 : 310  100 = 112,9 %
100 = 112,9 %
Процент снижения или увеличения себестоимости рассчитывается как (iz*100%) - 100%.
С помощью индивидуального индекса себестоимости можно определить сумму экономии (перерасхода) от снижения себестоимости продукции данного вида. Для каждого отдельного вида продукции сумма экономии (перерасхода) вычисляется по формуле:
iz = z1 - z0. (3)
Имеется возможность сравнивать суммы качественно однородных цифр за разные периоды, так как однородные по качественному признаку цифры являются сопоставимыми и соизмеримыми.
Индивидуальные индексы относятся к однородным ( по качественному признаку) объектам и поэтому для расчётов используется формула в следующем виде:
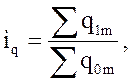 (4)
(4)
где iq – индивидуальный индекс количества чего-либо;
m – буквы или числа соответствующие различным однородным признакам.
▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼
|
▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲
По определению индивидуальный индекс не имеет весов. Характеристика «вес» или частота имеют важное значение при исчислении индексов и показывает повторяемость значений признака в совокупности. Используется система весовых характеристик только в сложных или агрегатных индексах.
Надо отметить, что отсутствие весов приводит к искажению экономического смысла значений полученных индексов.
Так, расчёты в примере 1 по вычислению общего изменения себестоимости по трём видам продукции с использованием зависимости (4) искажают результаты анализа себестоимости.
По количественному признаку себестоимость трёх неоднородных видов продукции в текущем и базисном периоде являются несоизмеримыми. Судя по величине iz= 96,2%, себестоимость выпуска трёх видов продукции уменьшилась на 3,8%. Однако это ошибочная величина. Несоизмеримость объектов привела к искажению результатов, к так называемому самовзвешиванию.
Поэтому индивидуальный суммарный индекс вычисляется только для качественно однородных элементов.
В целом рекомендуется применять индивидуальные индексы в случаях, когда:
1) вычисление индексов проводится по однородным группам элементов или объектов (товаров, видов продукции и т.п.) в процессе проведения статистического наблюдения за разные периоды времени или на разных территориях;
2) проводится расчёт гармонических агрегатных индексов (здесь необходимо наличие значений соответствующих индивидуальных индексов – цен, количества и т.п.)
При этом важно также учитывать соизмеримость цифровых данных для вычисления индивидуальных индексов. Несоизмеримость входных цифровых данных может привести к искажению конечных выводов в результате самовзвешивания числовых характеристик.
Покажем на примере, как правильно исчислять индивидуальные индексы при проведении статистического исследования цен товаров по двум территориям в различные периоды времени.
▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼
|
▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲
Итак, индивидуальные индексы выражают соотношение отдельных элементов совокупности. Так, если в прошлом году было произведено 55,4 млн т удобрений, в текущем 80,4 млн т, то это означает что в результате производство удобрений увеличилось в 1,45 раза (80,4/55,4), или на 45% больше. Это и есть индивидуальный индекс, характеризующий динамику производства удобрений.
Индекс как относительный показатель выражается в виде коэффициентов, когда база для сравнения принимается за единицу, и в процентах, когда база для сравнения принимается за 100.
Если в результате вычислений полученный индекс больше 1 или 100%, то это указывает на рост явления, если же меньше 1 или 100%, - на снижение уровня изучаемого явления. В приведенном выше примере индивидуальный индекс производства удобрений равен 1,45, или 145%, что свидетельствует о повышении производства на 45%.
1.3. Применение в экономическом анализе общих индексов в агрегатной форме
Если известно, что изучаемое явление не является однородным, то сравнение уровней возможно только после приведения их к общей мере. В этом случае анализ выполняется с использованием общих (агрегатных) индексов.
Агрегатный индекс – это сложно построенные индексы, включающие индексируемый показатель (индекс) и вес.
Такого типа индекс является формой сводного (общего) индекса, используемого для анализа изменения сложного экономического явления. «Агрегатным» он называется потому, что его числитель и знаменатель представляют собой набор – «агрегат» (от латинского aggregatus – складываемый, суммируемый) непосредственно несоизмеримых и не поддающихся суммированию элементов – суммы произведений двух величин. Одна из них меняется (индексируется), а другая – остается неизменной в числителе и знаменателе (вес индекса).
Вес индекса служит для соизмерения индексируемых величин. Благодаря наличию весов несоизмеримые (по величине, масштабу и др.) элементы становятся соизмеримыми.
Агрегатный индекс является основной формой индекса, так как в этом индексе отчетливо выступает отношение двух абсолютных величин, различающихся за счет изменения изучаемого явления.
Например, стоимость всей выработанной на предприятии продукции получается путем умножения на цену количества выпущенной продукции каждого вида и суммирования произведений по всем видам продукции. Тогда стоимость продукции базисного периода будет определена так:
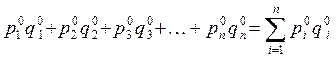 , (5)
, (5)
а стоимость продукции отчетного периода составит:
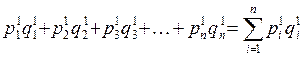 , (6)
, (6)
где 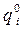 ,
, 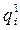 – количество единиц отдельных видов продукции, соответственно в базисном и отчетном периодах;
– количество единиц отдельных видов продукции, соответственно в базисном и отчетном периодах; 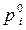 ,
, 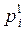 – цена единицы отдельных видов продукции соответственно в базисном и отчетном периодах;
– цена единицы отдельных видов продукции соответственно в базисном и отчетном периодах;  – количество отдельных видов продукции.
– количество отдельных видов продукции.
Если разделить стоимость продукции отчетного периода на стоимость продукции базисного периода, получим индекс стоимости продукции.
В общем виде его можно записать так:
 (7)
(7)
Если стоимость продукции в отчетном периоде выросла, то индекс стоимости будет больше 1, а если она снизилась – то меньше 1 [5, с. 343].
Величина агрегатного индекса физического объёма зависит от индивидуальных индексов, так как общее изменение объёма продукции есть результат изменения объёма производства каждого отдельного вида продукции. Общий результат изменения зависит также от удельного веса отдельных видов продукции в общем объёме выпуска.
Дата добавления: 2014-12-23; просмотров: 488; Мы поможем в написании вашей работы!; Нарушение авторских прав |
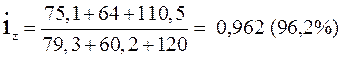 .
.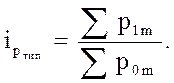
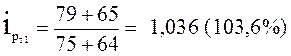 и по аналогии далее.
и по аналогии далее.