
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Показателей
Наряду с индексами физического объема продукции, в планировании и статистико-экономическом анализе деятельности предприятий и отраслей широко применяются индексы качественных показателей: цен, себестоимости, производительности труда, средней заработной платы и т. д. Качественный показатель характеризует уровень изучаемого результативного показателя в расчете на количественную единицу и определяется как отношение данного результативного показателя к связанному с ним количественному показателю (фактору). Так, себестоимость единицы продукции определяется как отношение суммы затрат на производство этого вида продукции к количеству единиц продукции данного вида. Средняя заработная плата определяется путем деления фонда заработной платы на численность работников и т. д.
Рассмотрим формулы индексов качественных показателей на примере расчета индексов цен по данным табл. 1.
Для определения общего изменения уровня цен на продукцию предприятия, включающую разные виды, нужно рассчитать агрегатный индекс цен.
Несоизмеримость уровней цен одного станка и одной тонны литья в таком случае преодолевается путем взвешивания цены каждого вида продукции на количество произведенных единиц, т. е. для отчетного и базисного периодов определяются величины вида  , которые и сравниваются между собой. Это сравнение будет отражать только изменение цен, если величина
, которые и сравниваются между собой. Это сравнение будет отражать только изменение цен, если величина  фиксировалась в числителе и знаменателе индекса цен на уровне одного из периодов. Общая формула агрегатного индекса цен записывается так:
фиксировалась в числителе и знаменателе индекса цен на уровне одного из периодов. Общая формула агрегатного индекса цен записывается так:
 . (11)
. (11)
Как и в случае построения агрегатных индексов физического объема, возможен выбор в качестве веса количества продукции отчетного периода 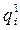 (формула Пааше) или количества продукции базисного периода
(формула Пааше) или количества продукции базисного периода  (формула Ласпейреса) [5].
(формула Ласпейреса) [5].
Формула агрегатного индекса цен Ласпейреса:
 . (12)
. (12)
Формула агрегатного индекса цен Пааше:
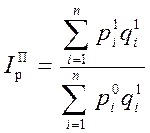 (13)
(13)
▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼

▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲
1.4. Построение общих индексов как средних
из индивидуальных
Помимо записи общих индексов в агрегатной форме, на практике часто используют формулы определения общих индексов как величин, средних из одноименных индивидуальных индексов. В этом смысле общий индекс изучаемого явления рассматривается как результат изменения уровня данного явления у отдельных единиц совокупности. В процессе осреднения индивидуальных индексов веса подбираются таким образом, чтобы был возможен алгебраический переход от общего индекса как средней величины к общему индексу в агрегатной форме. И наоборот, агрегатная форма общего индекса позволяет выбрать взвешивающий показатель при расчете общего индекса в виде средней величины. Эти преобразования, как правило, не сложны.
Так, индекс объема товарооборота может быть преобразован в форму средней арифметической взвешенной:
 . (14)
. (14)
Исходной базой построения средневзвешенного индекса физического объема продукции служит его агрегатная форма (формула (5)):
 . (15)
. (15)
Из имеющихся данных можно получить знаменатель этой формулы, для нахождения числителя используем формулу индивидуального индекса объема продукции  , по которой следует, что
, по которой следует, что  . Подставляя данное выражение в числитель агрегатной формы, получаем общий индекс физического объема в форме среднего арифметического индекса физического объема продукции, где весами служит стоимость отдельных видов продукции в базисном периоде (
. Подставляя данное выражение в числитель агрегатной формы, получаем общий индекс физического объема в форме среднего арифметического индекса физического объема продукции, где весами служит стоимость отдельных видов продукции в базисном периоде (  ):
):
 . (16)
. (16)
Если известны данные, позволяющие исчислить только числитель агрегатного индекса физического объема по формуле (5), то, аналогично выражая продукцию базисного периода, производим замену в знаменателе агрегатной формы. В результате получаем общий индекс физического объема в форме среднего гармонического индекса физического объема, где весами служит стоимость продукции отчетного периода в базисных ценах (  ):
):
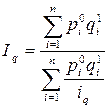 . (17)
. (17)
В форме средней гармонической индекс физического объёма используется только в аналитических целях [7, с. 308]
Аналогично происходит преобразование агрегатного индекса качественного показателя в средний гармонический и средний арифметический [2, с. 261, 264]. Например:
средний гармонический индекс цен, который тождественен формуле Пааше:
 , (18)
, (18)
средний арифметический индекс цен, тождественный агрегатному индексу Ласпейреса:
 . (19)
. (19)
При выборе весов следует иметь в виду, что средний индекс должен быть тождественен агрегатному, который является основной формой индекса [7].
▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼


▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲
Рассмотрим ещё один пример, иллюстрирующий другой входной тип информации для принятия решения о динамике реализации разноимённых товаров. Оценка и анализ выполняется также с использованием индексной системы.
▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼


▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲
1.5. Взаимосвязь цепных и базисных индексов
Для изучения динамики показателя за ряд периодов проведем вычисление с использованием системы цепных и базисных индексов. Расчет такой системы индексов может быть выполнен в двух вариантах:
1. Выполняя построение системы индексов с постоянной базой сравнения, получают базисные индексы. В этом случае сравнивают размер показателя в различные периоды с уровнем того же показателя в определенный постоянный период времени.
2. Формируя систему индексов с переменной базой сравнения – цепные индексы) [2]. При этом оценивают относительное изменение уровня изучаемого явления по сравнению с предыдущим периодом.
В табл. 4 приведено структурное табличное обобщение системы цепных и базисных индексов на примере физического объема товарооборота, цен и стоимости продукции.
Таблица 4
| Индексы | Базисные | Цепные | |||||||
| Физического объема продукции | индивидуальные | 
| 
| 
| 
| 
| 
| 
| 
|
| агрегатные | в ценах базисного периода | 
| 
| 
| 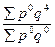
| 
| 
| 
| 
|
| в ценах отчетного периода | 
| 
| 
| 
| 
| 
| 
| 
| |
| Цен | индивидуальные | 
| 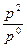
| 
| 
| 
| 
| 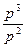
| 
|
| агрегатные | с весами базисного периода | 
| 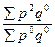
| 
| 
| 
| 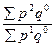
| 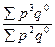
| 
|
| с весами отчетного периода | 
| 
| 
| 
| 
| 
| 
| 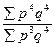
| |
| Стоимости | индивидуальные | 
| 
| 
| 
| 
| 
| 
| 
|
| агрегатные | 
| 
| 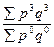
| 
| 
| 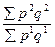
| 
| 
|
Допустим, имеются данные об объеме продукции в натуральном выражении и уровне цен на эту продукцию за пять периодов (0, 1, 2, 3, 4 – номера периодов).
Для индивидуальных индексов цен, индексов физического объема и индексов стоимости продукции справедливо следующее правило:
1) произведение промежуточных по периодам цепных индексов дает базисный индекс последнего периода:
i4/0= i1/0 i2/1 i3/2 i4/3 ; (20)
2) отношение базисного индекса отчетного периода к базисному индексу предшествующего периода дает цепной индекс отчетного периода:
i4/3= i4/0 : i3/0 . (21)
Это правило позволяет применить так называемый цепной метод, т. е. находить неизвестный ряд базисных индексов по известным цепным и наоборот.
Рассмотрим возможность применения цепного метода исчисления для агрегатных индексов. Цепной индекс отчетного периода можно получить, имея два базисных агрегатных индекса физического объема с постоянным соизмерителем (цены базисного периода  ):
):
 (22)
(22)
Базисный индекс отчетного периода может быть получен путем перемножения соответствующих цепных индексов, если соизмеритель (цена) принимается на уровне одного и того же периода
 (23)
(23)
Использование цепного метода для агрегатных индексов физического объема оказалось возможным благодаря применению в качестве соизмерителя фиксированных (сопоставимых) цен.
Если воспользоваться другим вариантом построения индекса физического объема (табл. 4), то нельзя получить точного значения базисного индекса путем перемножения соответствующих цепных индексов, так как при исчислении каждого следующего индекса цены меняются: получается ряд индексов с меняющимся соизмерителем:
 (24)
(24)
Таким образом, при использовании переменных соизмерителей цепной метод для расчета базисных агрегатных индексов физического объема применить нельзя.
Агрегатные индексы качественных показателей, рассчитанные по формуле Пааше, всегда являются индексами с меняющимися весами, так как количество продукции каждый раз принимается на уровне отчетного периода (табл. 6 – индексы цен с весами отчетного периода). Поэтому цепной метод расчета индексов неприменим к таким агрегатным индексам качественных показателей.
Базисные индексы могут быть определены на основе цепных, а цепные индексы могут быть рассчитаны с помощью базисных индексов, если воспользоваться формулой Ласпейреса для расчета агрегатных индексов цен при условии постоянных весов  для всех периодов (табл. 4 – индексы цен с весами базисного периода).
для всех периодов (табл. 4 – индексы цен с весами базисного периода).
При исчислении цепных агрегатных индексов физического объема (табл. 6) может быть применена и другая система измерителей [5].
Так, при исчислении отдельных индексов используются цены периода, предшествующего отчетному. Тогда получают следующий ряд цепных индексов:

То же самое может быть и при определении цепных агрегатных индексов цен с весами базисного периода. В качестве веса могут использоваться физические объемы продукции периода, предшествующего отчетному.
Сформулированное выше правило взаимосвязи цепных и базисных индивидуальных индексов в полном объеме применимо к агрегатным индексам стоимости.
▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼


▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲
Для общих индексов свойства связи между базисными и цепными индексами справедливо только, если ряд общих индексов рассчитан с одними и теми же весами.
▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼


▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲
Дата добавления: 2014-12-23; просмотров: 367; Мы поможем в написании вашей работы!; Нарушение авторских прав |