
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Глава 3. использование Индексов при анализе структурных изменений явлений
На динамику качественных показателей, уровни которых выражены средними величинами, оказывает влияние изменение структуры изучаемого явления, в виде различной степени воздействия факторов, связанных с их долей участия в этом процессе.
3.1. Индексы средних величин
Изменение структуры явления – это изменение доли отдельных единиц совокупности, из которых формируются средние, в общей их численности. Например, средняя производительность труда на предприятии может возрасти за счет ее повышения у отдельных рабочих и увеличения доли рабочих с более высокой производительностью труда в общей численности рабочих, вырабатывающих одноименную продукцию. При этом могут наблюдаться случаи повышения средней производительности труда при снижении ее у отдельных рабочих. Такое повышение будет обеспечено увеличением доли рабочих с более высокой производительностью труда, т. е. структурным сдвигом.
Для характеристики изменения структуры совокупности в динамике может быть использован интегральный коэффициент структурных различий А. Салаи:
 , (38)
, (38)
где 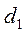 ,
,  – относительные показатели структуры изучаемых совокупностей в отчетном и базисном периодах соответственно;
– относительные показатели структуры изучаемых совокупностей в отчетном и базисном периодах соответственно; 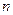 – число структурных групп.
– число структурных групп.
По значению коэффициента судят о происшедших изменениях в составе сравниваемых совокупностей.
Если  – произошли максимальные различия
– произошли максимальные различия
Если 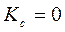 – полное совпадение сравниваемых структур.
– полное совпадение сравниваемых структур.
Изменение коэффициента от 0 до 1 показывает меру структурных различий изучаемых совокупностей [1, с. 184].
На изменение динамики среднего значения изучаемого явления могут оказывать влияние одновременно два фактора: изменение значений усредняемого показателя и изменение структуры явления. В связи с этим различают индексы переменного и фиксированного состава. В этом случае задача состоит в определении степени влияния этих факторов. Для ее решения используется индексный метод, т. е. строится система взаимосвязанных индексов, в которую включается три индекса: переменного состава, постоянного состава и структурных сдвигов.
Изучение совместного действия этих двух факторов на общую динамику среднего уровня осуществляется в статистике с помощью индекса переменного состава. Он представляет собой отношение двух взвешенных средних с изменяющимися весами, показывающее изменение индексируемой средней величины.
Для любых качественных показателей индекс переменного состава можно записать в общем виде:
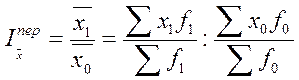 , (39)
, (39)
где 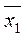 ,
, 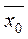 – средние уровни усредняемого показателя в отчетном и базисном периодах соответственно;
– средние уровни усредняемого показателя в отчетном и базисном периодах соответственно;  ,
, 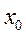 – текущие уровни явления,
– текущие уровни явления,  ,
, 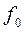 – веса усредняемого показателя в отчетном и базисном периодах соответственно.
– веса усредняемого показателя в отчетном и базисном периодах соответственно.
Чтобы элиминировать влияние изменения структуры совокупности на динамику средней величины, берут отношение средних взвешенных с одними и теми же весами (как правило, на уровне отчетного периода). Индекс, характеризующий динамику средней величины при одной и той же фиксированной структуре совокупности, называется индексом постоянного (фиксированного) состава и исчисляется в общем виде:
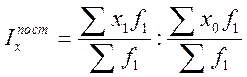 . (40)
. (40)
После сокращения на  формула принимает вид формулы агрегатного индекса качественного показателя:
формула принимает вид формулы агрегатного индекса качественного показателя:
 (41)
(41)
Индекс постоянного состава показывает, как в отчетном периоде по сравнению с базисным изменилось среднее значение показателя по какой-либо однородной совокупности за счет изменения только самой индексируемой величины, т. е. когда влияние структурного фактора устранено.
Для измерения влияния только структурных изменений на исследуемый средний показатель исчисляют индекс структурных сдвигов как отношение среднего уровня индексируемого показателя базисного периода, рассчитанного на отчетную структуру, к фактической средней этого показателя в базисном периоде:
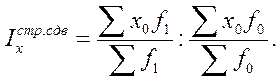 (42)
(42)
В качестве весов индексов средних величин, наряду с абсолютными показателями, могут использоваться и относительные показатели (доли):
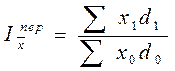 ;
; 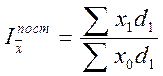 ;
; 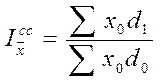 ,
,
где 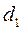 ,
,  – доли единиц с определенным значением признака в общей совокупности в отчетном и базисном периодах соответственно
– доли единиц с определенным значением признака в общей совокупности в отчетном и базисном периодах соответственно

Рассмотрим использование приведенных зависимостей.
▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼


▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲
Выполним пример, когда в условии задания приводятся значения сопряжённых показателей. В этом случае надо быть очень внимательными при использовании зависимостей индексной системы.
▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼


▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲
3.2. Особенности учета структурных изменений при построении системы индексов
Система индексов, которая строится по типу индексов физического объема, применима как при изучении совокупностей, состоящих из объектов разных типов, так и для совокупностей, состоящих из объектов одного и того же типа.
Если совокупность неоднородна (например, совокупность товаров различного вида), то индекс физического объема – единственный способ показать динамику такой массы различных предметов, выражая ее через взвешивающий множитель (цену, себестоимость, трудоемкость). Если совокупность состоит из объектов одинакового типа, то динамику этого массива можно оценить, сравнивая общее количество составляющих в отчетном периоде с их аналогичной величиной в базисном.
Так, для рассмотренного выше случая(►9, с.41), можно определить не только IT индекс изменения объема продукции в связи с изменением общей численности работающих, но и индекс изменения общей численности:

Рассмотрим соотношение между индексами IT и IΣT. В формуле для IT разделим и умножим числитель на ΣТ1а знаменатель на ΣТ0:
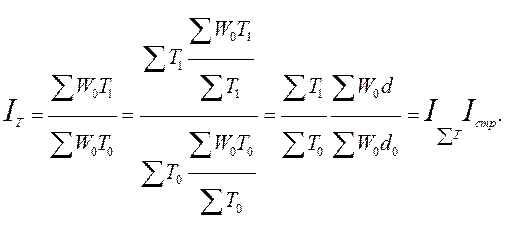
Так, для однородных совокупностей (допускающих суммирование по количественному признаку) индекс физического объема есть произведение индекса суммарной численности совокупности на индекс изменения структуры. Формула индекса структурных изменений для нашего примера
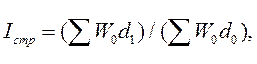
где d0, d1 , - удельные веса или доли предприятий в общей численности работающих соответственно в базисном и отчетном периодах.
При этом
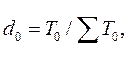
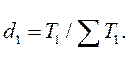
Знаменатель в формуле индекса структурных изменений есть не что иное, как средний уровень выработки по группе предприятий в базисном периоде, так как
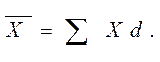
Индекс структурных изменений показывает, во сколько раз изменился общий средний уровень (в данном случае уровень выработки) только за счет изменения удельного веса каждого объекта (предприятия) в общем объеме количественного признака (в данном случае в общей численности рабочих).
В той же мере индекс влияния структурных изменений показывает влияние процессов перераспределения на общий прирост итогового показателя (в данном случае на общий прирост продукции).
▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼
|
| ||||||||||||||||||||||||
|
▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲
Вклад каждого фактора в общий прирост можно перераспределить и по отдельным субъектам. Для этого к каждому объекту в отдельности применяют мультипликативную индексную модель:

где q0,q1 - объемы итогового признака (продукции) по данному объекту (предприятию);
IΣT - общий для всей совокупности индекс количественного признака (индекс числа работающих);
iW- индивидуальный для данного объекта индекс изменения уровня качественного признака (индивидуальный индекс производительности труда для данного предприятия);
id- индивидуальный индекс доли данного объекта в общем объеме количественного признака (индивидуальный индекс доли данного предприятия в общей численности работающих).
Индивидуальный индекс доли можно определить и по первичным данным, сопоставляя удельные веса за отчетный и базисный периоды.
Действительно,

При изучении совокупностей, состоящих из объектов одного и того же типа, общий индекс изменения итогового признака можно, как показано выше, представить произведением трех индексов:
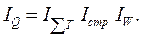
Индекс IW можно записать как
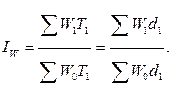
Теперь мультипликативная индексная модель выглядит следующим образом:
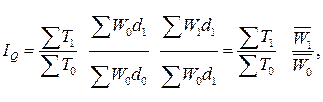
или
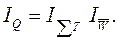
Отношение двух средних величин называется индексом переменного состава. Этот индекс учитывает одновременно и структурные изменения в составе совокупности, и изменение уровня качественного признака у отдельных объектов.
В этом смысле рассчитанный ранее индекс IW, (полученный по типу индекса цен) называется индексом постоянного, или фиксированного состава. Очевидно, что между двумя названными индексами существует соотношение
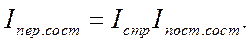
В нашем примере это выразится как
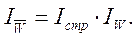
Представление индекса переменного состава произведением двух сопряженных индексов позволяет выяснить роль соответствующих факторов в изменении общего среднего уровня качественного показателя.
▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼
|
▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲
В целом, владея инструментарием построения индексной системы и зная особенности учёта особенностей отражения структурных изменений, можно проводить более глубокий и осмысленный анализ динамики экономических явлений и процессов.
Глава 4. СИСТЕМА ВЗАИМОСВЯЗАННЫХ ИНДЕКСОВ ПРИ ФАКТОРНОМ АНАЛИЗЕ
Ранее при помощи индексов рассматривалась двухфакторная связь, то есть связь между результативным и двумя факторными признаками. На практике общий индекс может зависеть от большего числа факторов: трёх, четырёх и более, т.е. связь может быть трёхфакторной, четырёхфакторной и т.д. В этом случае построение системы индексов требует применения определённых правил, которые описаны в данной главе.
4.1. Построение многофакторных моделей
При построении многофакторных моделей должна соблюдаться определенная последовательность в использовании и записи факторов. В основу формирования индексной модели должно быть положено определенное экономическое содержание произведений двух смежных факторов. После чего может быть осуществлено преобразование (свертывание) сложной многофакторной модели в модель, содержащую меньшее число факторов, что облегчает обоснование выбора весов или соизмерителей соответствующих показателей.
Так, стоимость материальных затрат для производства определённой продукции зависит от стоимости сырья, его расхода на единицу продукции и от количества выпущенной продукции. Изменение одного из указанных факторов повлечёт за собой изменение результата – всех затрат на выпуск продукции. Следовательно, изучая динамику такого сложного результативного показателя, важно правильно построить систему взаимосвязанных признаков.
Если обозначить факторные признаки за q, х, у, а результативный за z, то система взаимосвязанных индексов будет иметь следующий вид:
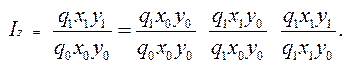 (43)
(43)
Факторные индексы построены так, что они составляют взаимосвязанную систему, не изолированную друг от друга.
В формуле (33) индекс объёма (количества выпущенной продукции)  построен при фиксированном расходе и ценах на уровне базисного периода, индекс удельных расходов
построен при фиксированном расходе и ценах на уровне базисного периода, индекс удельных расходов 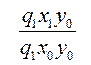 − при фиксировании объёма продукции на уровне отчётного периода, а цен на уровне базисного периода, индекс цен
− при фиксировании объёма продукции на уровне отчётного периода, а цен на уровне базисного периода, индекс цен
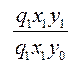 − при фиксировании удельного расхода и объёма продукции на уровне отчётного периода.
− при фиксировании удельного расхода и объёма продукции на уровне отчётного периода.
Для получения суммы абсолютного прироста за счёт соответствующего фактора, необходимо произвести вычитание из числителя каждой формулы её знаменатель.
В построенной системе взаимосвязанных индексов для первого факторного индекса (объёма) зафиксированы показатели расхода и цены на уровне базисного периода, так как объём является количественным показателем. Для второго факторного индекса (расходов) влияние изменения норм на общие затраты указано с учётом изменения объёма, а цены на отчётный выпуск продукции остаются по-прежнему неизменными. И завершающий третий факторный индекс (цен) построен с постоянными весами на уровне отчётного периода объёма продукции и удельных расходов, так как цена является качественным показателем.
Важным является то, что чем больше взаимосвязанных факторов определяют результативный показатель, тем более сложным является процесс разложения по факторам. Тем большего обоснования и аргументации требует процесс построения каждого из факторных индексов.
Оценим стоимость экспорта (среднюю внешнеторговую цену), на который влияет физический объём экспорта qi, торговая цена pj и географическая оставляющая структуры экспорта dj.
При построении трёхфакторной модели при оценке влияния одного из факторов на изменении результативного показателя два других фиксируются на уровне одного и того же периода.
Выбор периода, на уровне которого фиксируются значения факторов, зависит от того, каким показателем он является (количественным или качественным) по отношению к факторам, влияние которых оценивается. Так, при оценке влияния уровня цен на изменение экспортной выручки два других фактора структуры экспорта dj и объёма экспорта qi фиксируются на уровне отчётного периода, так как они являются количественными факторами по отношению к цене.
Модель, характеризующая среднюю экспортную цену соответствующего периода, представляет собой сумму произведений внешнеторговой цены на долю поставок в j-ю страну 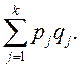 В этой двухфакторной модели pj является качественным показателем, dj – количественным. Следовательно, при определении влияния структуры физического объема товарооборота на изменение экспортной выручки pj будет фиксироваться на уровне базисного периода. Величина физического объема товарооборота по отношению к средней цене экспорта является количественным фактором, поэтому будет фиксироваться на уровне отчетного периода (фактор dj, влияние которого оценивается, входит в величину средней цены экспорта).
В этой двухфакторной модели pj является качественным показателем, dj – количественным. Следовательно, при определении влияния структуры физического объема товарооборота на изменение экспортной выручки pj будет фиксироваться на уровне базисного периода. Величина физического объема товарооборота по отношению к средней цене экспорта является количественным фактором, поэтому будет фиксироваться на уровне отчетного периода (фактор dj, влияние которого оценивается, входит в величину средней цены экспорта).
▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼
| |||
|
▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲
Примером мультипликативной модели с большим числом факторов является также изменение общей суммы материальных затрат на производство продукции. Сумма затрат изменяется вследствие изменения количества выпущенной продукции (индекс  ), изменения удельных расходов материала на единицу продукции (индекс
), изменения удельных расходов материала на единицу продукции (индекс 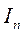 ), изменения цены на материал (индекс
), изменения цены на материал (индекс  ).
).
Прирост общей суммы затрат распределится как

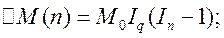
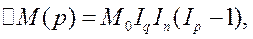
где
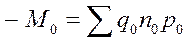 ,
,
а величины индексов определяются следующим образом:
- индекс увеличения суммы затрат в связи с изменением объемов производства продукции (индекс физического объема)
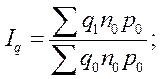
- индекс изменения суммы затрат за счет изменения удельных расходов материала (индекс удельных расходов)
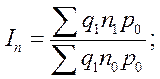
- индекс изменения общей суммы затрат на материалы, объясняемый изменением цен на материалы (индекс цен на материалы)
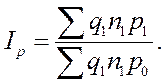
Помимо влияния факторов на результат в абсолютном выражении можно определить относительный размер их влияния.
4.2. корректировка индексов
в мультипликативной модели
Рассмотрим процедуру разложения темпа прироста некоторого сложного фактора на составляющие, на примере стоимости экспорта по определяющим его факторам.
Определим, как будет изменяться стоимость экспорта за счет изменения физического объема экспорта и за счет роста уровня средних цен экспорта. Для этого преобразуем абсолютный прирост стоимости экспорта под влиянием изменений каждого из факторов, опираясь на двухфакторную модель взаимосвязи названных выше показателей:
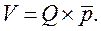 (44)
(44)
Тогда за счет изменения всех факторов, входящих в модель, абсолютный прирост экспорта будет определяться из зависимости:
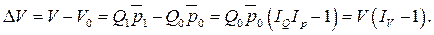 (45)
(45)
За счет изменения фактического объема экспорта его величина составит:
 (46)
(46)
А из-за изменения только уровня средних цен стоимость экспорта будет:
 (47)
(47)
Полученные зависимости могут быть использованы для расчета темпов прироста стоимости экспорта. При этом надо учитывать, что темп прироста получают путем деления абсолютного прироста на уровень базисного периода.
При однонаправленном изменении факторов, формирующих результативный показатель, может быть рассмотрена структура темпа прироста результативного показателя, т. е. определена доля каждого фактора в общем приросте:
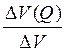 и
и 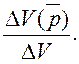
Используя выражения (42) – (44), определим относительный размер влияния каждого фактора:
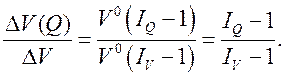 (48)
(48)
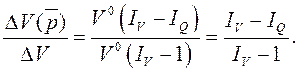 (49)
(49)
Выполним пример, реализующий полученные зависимости.
▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼


▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲
Рассмотрим далее вопросы корректировки индексов в мультипликативных моделях.
Прирост итогового показателя в упорядоченной последовательности факторов за счет определенного фактора в процессе индексного анализа определяется как
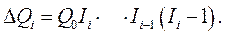 (50)
(50)
Из формулы видно, что прирост за счет конкретного фактора может быть либо положительным, если соответствующий индекс больше единицы, либо отрицательным, если этот индекс меньше единицы. Эта особенность индексного анализа может существенно усложнить интерпретацию полученных результатов. Если знаки всех частей общего прироста совпадают (т.е. либо все индексы больше единицы, либо все меньше единицы), то соответствующие приросты показывают роль каждого фактора либо в положительном приращении, либо в снижении итогового показателя.
Если направления абсолютных приростов по факторам не совпадают, то на основе индексной модели можно получить такое разложение общего прироста итога, что его абсолютный прирост будет равен сумме абсолютных значений факторных приростов:
 (51)
(51)
Таким образом, сумма абсолютных значений пофакторных приростов будет равна абсолютному значению прироста итогового признака.
Например, пусть DQ > 0 (при Q1 > Q0). Отметим индексы, меньшие единицы и найдем их произведение — Пm=обозначим за m число индексов, меньших единицы. Заменим все отмеченные индексы на единицу, а все оставшиеся большие единицы, умножим на коэффициент 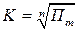 где n — число индексов, больших единицы. Если в полученной последовательности скорректированных индексов некоторые снова оказались меньше единицы, то процедуру повторяем. В итоге имеем последовательности индексов, каждый из которых не меньше единицы, что обеспечивает однозначность разложения общего прироста.
где n — число индексов, больших единицы. Если в полученной последовательности скорректированных индексов некоторые снова оказались меньше единицы, то процедуру повторяем. В итоге имеем последовательности индексов, каждый из которых не меньше единицы, что обеспечивает однозначность разложения общего прироста.
Для случая DQ < 0 аналогичная процедура выполняется по обратным значениям индексов и по «перевернутой» модели.
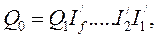
при
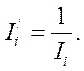
Как видно из предыдущего, индексный анализ – разделение общего прироста итогового показателя по факторам – проводится только по данным о конечных результатах развития явления: используются итоговые данные базисного периода (например, объем продукции и численность работающих) и аналогичные показатели отчетного периода. Чтобы выполнить анализ, необходимо предварительно решить вопрос об очередности, последовательности влияния факторов, определяющих динамику итога. Затем рассчитываются индексы этих факторов и далее в соответствии с очередностью влияния распределяется общий прирост итогового показателя.
В классической схеме индексного анализа очередность влияния факторов предполагается единственной: количественные факторы по своему воздействию на итог предшествуют качественным. Очевидно, что классическая схема анализа представляет лишь один из возможных вариантов очередности. Если имеется F факторов (индексов), то при отсутствии информации о фактической динамике явления, когда и индексы, и величина итогового признака становятся известными лишь по конечному результату всего периода, любая последовательность влияния факторов в мультипликативной индексной схеме оказывается равновероятной. Всего таких вариантов очевидно будет F!. Рассмотрим эту ситуацию на примере простых индексных систем, когда значения индексов не зависят от их местоположения в цепи сомножителей мультипликативной модели.
Равновероятное влияние отдельного фактора определится, если рассчитать его вклад в общий прирост для всех F! вариантов перестановки индексов в модели:

Любой интересующий нас индекс (фактор) с номером i может оказаться (F-1)! раз на любом из F мест.
Каждому местоположению индекса соответствует (F-1)! значений прироста итогового показателя (среди них могут быть и равные). Например, для модели с четырьмя индексами
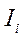 ,
, 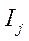 ,
, 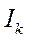
 ,
,
рассчитывая прирост по фактору i имеем :
1. Индекс на первом месте. Прирост итога рассчитывается шесть раз по формуле
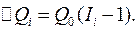
2. Индекс на втором месте. Прирост итога определяется два раза по формуле

два раза по формуле
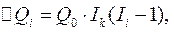
и два раза по формуле
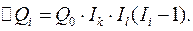
3. Индекс на третьем месте. Прирост итога определится два раза по формуле

два раза по формуле

и два раза по формуле
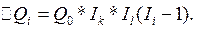
4. Индекс на четвертом месте. Прирост итога рассчитывается шесть раз по формуле
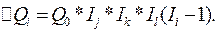
Суммируя все варианты и определяя среднее значение, получаем формулу вклада фактора i в общий прирост итога для четырехфакторной модели:
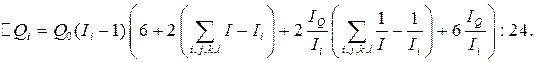
В общем случае для модели с F факторами в прямом переборе нет необходимости. Формулу для модели с F факторами можно сконструировать по формуле равновероятного прироста для модели с (F-1) факторами. Процесс образования формул проиллюстрирован на схеме.
1.    1. 1.   ( 1 ) :1;
2. ( 1 ) :1;
2.  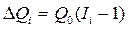  (1 + (1 + 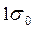 ) :2 ) :2
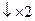 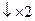 3.
3.   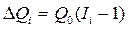  (2 + (2 + 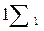 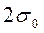 ) :6 ) :6
 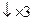 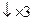 4.
4. 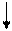 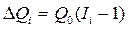  ( ( 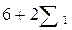 + + 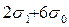 ) :24 ) :24
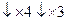 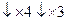 5.
5.    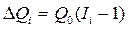  ( (  + +  + +  ) :120 ) :120
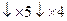 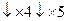 6.
6. 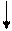 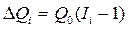  ( ( 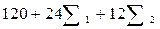 + + 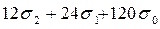 ) :6 ) :6
  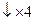 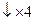   7.
7. 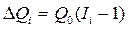  ( ( 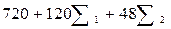 + +  + +  ):6 ):6
|
Рис.2. Схема-конструкция формул равновесного прироста.
На рис. 2 стрелками показано образование коэффициентов. Следует обратить внимание на образование коэффициента при центральном слагаемом – в случае нечетного числа факторов коэффициент при центральном слагаемом образуется из аналогичного коэффициента предыдущей модели с нечетным числом факторов умножением на ((F-1)/2)2 .
На схеме символом Σn обозначено выражение
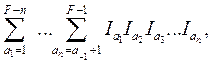 причем
причем 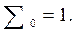
Символом σn обозначено выражение
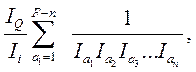 , причем
, причем

В этих выражениях F - число факторов модели, IQ- индекс итогового показателя, Ii- индекс фактора, по которому рассчитывается прирост итога.
Операции суммирования при расчете Σn и σn ведутся по модифицированной последовательности индексов: из исходной последовательности удаляется индекс интересующего нас признака, остальные индексы перенумеровываются заново, проводится расчет Σn и σn , по завершении расчета прироста по фактору i восстанавливается исходная последовательность индексов-сомножителей.
Более сложная ситуация возникает, когда проводится индексный анализ по совокупности объектов. В этих случаях выбор очевидности влияния факторов задает не только схему разложения прироста, но и способ расчета агрегатного индекса, его значение.
Так, индекс структурных изменений может быть рассчитан и до, и после изменения выработки по предприятиям. Точно так же и индекс производительности постоянного состава может быть определен и по базисной, и по отчетной структурам. Единственно реальным способом анализа в этих случаях оказывается определение равновероятных значений прироста по факторам для каждого объекта совокупности, а затем подведение итогов по каждому фактору. Так, для случаев анализа общего прироста продукции по совокупности предприятий по каждому из них анализ проводится самостоятельно.
Для трехфакторной индексной модели  равновероятный прирост по любому из факторов, например по фактору i, находится как
равновероятный прирост по любому из факторов, например по фактору i, находится как
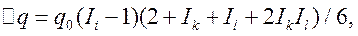
при i, k, l = 1,2,3, i ≠ k ≠ l .
Для рассмотренного ранее примера (с.36) полезно проанализировать полученные результаты о распределении прироста продукции по предприятиям (тыс. руб.):
▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼
|
▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲
Изложенный материал представляет значительный интерес для дальней шей разработки и развития практики его использования в практической деятельности всякого рода бизнеса.
РЕЗЮМЕ
Индекс - относительная величина, показывающая во сколько раз уровень изучаемого явления в определённых условиях отличается от уровня этого же явления в других условиях. Различие условий может проявляться во времени (индексы динамики), в пространстве (территориальные индексы), в выборе в качестве базы сравнения какого-либо условного уровня, например, планового показателя, уровня договорных обязательств и т.п.
Относительная величина, получаемая при сравнении уровней, называется индивидуальным индексом, если исследователь не интересуется структурой изучаемого явления и конкретную количественную оценку уровня в данных условиях сравнивает с такой же конкретной величиной уровня изучаемого явления в других условиях.
Если изучаемое явление неоднородно и сравнение уровней возможно только после приведения их к общей мере, экономический анализ выполняют с использованием общих индексов. Индекс становится общим, когда в расчетной формуле отражена неоднородность изучаемой совокупности. Примером неоднородной совокупности является общая масса проданных товаров всех или нескольких видов. Тогда сумма выручки запишется в виде агрегата (суммы произведений взвешивающего показателя на объемный показатель).
Отношение агрегатов, построенных для разных условий, дает общий индекс показателя в агрегатной форме. В зависимости от методологии расчета различают агрегатные и средние индексы.
При анализе динамики (выполнения плана и территориальных сравнений) среднего уровня качественного показателя задача решается путём построения системы взаимосвязанных индексов. Общий индекс, отражающий динамику среднего уровня за счет изменения обоих факторов (самих уровней и структуры совокупности), называется индексом переменного состава. Этот индекс позволяет учитывать два факторных индекса – сомножителя. Каждый из них отражает изменения только одного фактора и тем самым оценивается влияние этого изменения на общую динамику среднего уровня. В этом случае формируются индекс фиксированного (постоянного) состава и индекс влияния структурных сдвигов на динамику среднего уровня.
Существует общая рекомендация, выработанная практикой: в расчетах агрегатных индексов при индексировании вторичных признаков взвешивание обычно производится по отчетным весам, а первичных признаков - по базисным весам. Это обеспечивает увязку сопряженных индексов в системе и повышает их аналитические возможности.
В приложении приведен сквозной пример использования индексной системы для анализа влияния изменения средней численности работников на показатель товарооборота предприятия.
В этом разделе приведено:

| v Понятие об индексной системе. |
v Общие правила построения индивидуальных индексов.
v Принципы расчёта количественных, качественных и сопряжённых индексов-показателей.
v Основы взаимосвязи базисных и цепных индексов.

| v Особенности построения индексных систем по видам ( в т.ч. территориальных). v Особенности учёта структурных изменений с использованием системы средних индексов. v Основы построения и применения многофакторных индексных моделей. v Правила корректировки индексов в мультипликативных индексных моделях. v Большое число практических примеров по всей приведенной тематике. |
______________________________________________
Дата добавления: 2014-12-23; просмотров: 1424; Мы поможем в написании вашей работы!; Нарушение авторских прав |
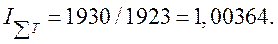 Влияние структурных сдвигов на средний уровень выработки и на общий прирост продукции определяется индексом
Влияние структурных сдвигов на средний уровень выработки и на общий прирост продукции определяется индексом
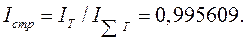 Для другого, более полного варианта расчета Iстр определяется доля каждого предприятия в общей численности работающих в базисном и отчетном периодах:
Таблица 14
Для другого, более полного варианта расчета Iстр определяется доля каждого предприятия в общей численности работающих в базисном и отчетном периодах:
Таблица 14
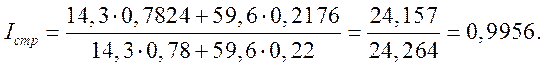
 Согласно этой модели, общий прирост продукции состоит, из трех частей:
1. Прирост за счет изменения общей численности работающих
Согласно этой модели, общий прирост продукции состоит, из трех частей:
1. Прирост за счет изменения общей численности работающих
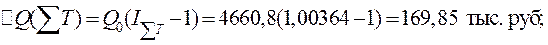 2. Прирост за счет перераспределения работающих
2. Прирост за счет перераспределения работающих
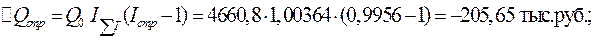 3.Прирост за счет изменения уровня производительности труда на предприятиях
3.Прирост за счет изменения уровня производительности труда на предприятиях 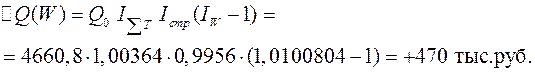 Из расчета видно, что основная причина снижения объема продукции при росте общей численности работающих - неблагоприятные структурные изменения. Снижение удельного веса по второму предприятию, где отмечается более высокий по сравнению с первым предприятием уровень выработки, привело к общему уменьшению выпуска продукции на 0,6%, что не компенсировалось его возрастанием на 0,4% за счет увеличения числа работающих.
В условиях нашего примера имеем:
Таблица 15
Из расчета видно, что основная причина снижения объема продукции при росте общей численности работающих - неблагоприятные структурные изменения. Снижение удельного веса по второму предприятию, где отмечается более высокий по сравнению с первым предприятием уровень выработки, привело к общему уменьшению выпуска продукции на 0,6%, что не компенсировалось его возрастанием на 0,4% за счет увеличения числа работающих.
В условиях нашего примера имеем:
Таблица 15
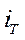

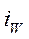
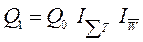 ,
но ничего нового по сравнению с ранее полученными результатами (табл. 16 ) этот подход уже не дает ◄
,
но ничего нового по сравнению с ранее полученными результатами (табл. 16 ) этот подход уже не дает ◄
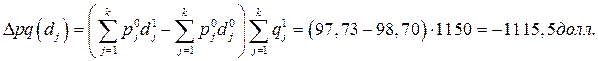 Данное значение товарооборота означает, что неблагоприятные изменения в географической структуре физического объема экспорта привели к снижению экспортной выручки на 1115,5 долл.
И наконец, изменение третьего фактора – физического объема экспорта – привело к увеличению экспортной выручки на 14 805 долл.:
Данное значение товарооборота означает, что неблагоприятные изменения в географической структуре физического объема экспорта привели к снижению экспортной выручки на 1115,5 долл.
И наконец, изменение третьего фактора – физического объема экспорта – привело к увеличению экспортной выручки на 14 805 долл.:

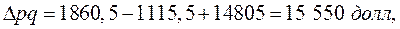 т. е. общая величина экспортной выручки под влиянием всех факторов возросла на 15 550 долл.
Выполненное разложение абсолютного прироста выручки от экспорта показало, что упущенная выгода в связи с изменением географической структуры экспорта составила 1115,5 долл., а основным фактором, повлиявшим на изменение стоимостного объема экспорта, было увеличение его физического объема [14]. ◄
т. е. общая величина экспортной выручки под влиянием всех факторов возросла на 15 550 долл.
Выполненное разложение абсолютного прироста выручки от экспорта показало, что упущенная выгода в связи с изменением географической структуры экспорта составила 1115,5 долл., а основным фактором, повлиявшим на изменение стоимостного объема экспорта, было увеличение его физического объема [14]. ◄