Построения индексных моделей

Способы построения индексов зависят от содержания изучаемых показателей, методологии расчета исходных статистических показателей, имеющихся в распоряжении исследователя статистических данных и целей исследования. Индексы могут относиться либо к отдельным элементам сложного экономического явления, либо ко всему явлению в целом.

Труднейший вопрос при построении индекса - выбор его весов и возможно более точное исчисление веса каждой группы, иногда и каждой единицы, входящей в индексируемую совокупность. Система таких весов должна отображать модель структуры того социально-экономического явления, динамика которого находит числовое выражение в индексе. Так, веса индекса цен должны отражать товарную структуру торгового оборота (розничного, оптового), весами бюджетного индекса должны быть натуральные количества товаров и услуг, входящих в бюджетный набор, и т.п. В индексе физического (натурального) объема роль весов для натуральных количеств играют неизменные цены, благодаря которым становится возможным "соизмерить" и свести воедино все части разносоставной натуральной совокупности; отсюда - часто общая, однако неправомерная трактовка любых видов индексов как "коэффициентов соизмерения" частей разносоставной совокупности.

2.1. Принципиальные основы выбора формы

индекса

Если подходить к принципам построения индексов с формально-математических позиций, ориентируясь на принцип элиминирования влияния других факторов, кроме изучаемого, при исчислении индексов можно опираться на веса базисного периода (формула Ласпейреса) или же на веса отчетного периода (формула Пааше). Используя эти два варианта построения индексов, Фишер предложил рассчитать среднюю геометрическую из двух агрегатных индексов – «идеальную формулу». В табл. 9 представлены варианты расчета агрегатных индексов физического объема и цен, наиболее часто используемых для характеристики временных или пространственных изменений в уровнях анализируемых показателей [5, с. 359].

Таблица 9

Варианты расчета агрегатных индексов физического объема и цен

Название индекса	Агрегатные индексы
Физического объема	Цен
Индекс с базисными весами (формула Ласпейреса)
Индекс с весами отчетного периода (формула Пааше)
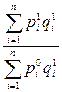
«Идеальная» формула Фишера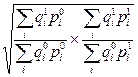

Основные факторы, влияющие на принятие решения по методу расчета агрегатного индекса, определены целями исследования, возможностями получения статистической информации, а также потребностями удешевления затрат на ее получение.

Предпочтение может быть отдано индексу Ласпейреса, если ориентироваться на синтетическое направление в использовании индексов, т. е. поставить задачу характеристики общего изменения уровня анализируемого показателя.

Например, при исчислении агрегатного индекса физического объема продукции в этом случае достаточно вести мониторинг за изменением физических объемов продукции, тогда как при использовании варианта агрегатного индекса Пааше должно учитываться изменение и физического объема продукции и цен.

Расчет агрегатного индекса физического объема продукции по формуле Ласпейреса получил наибольшее распространение в мировой практике. Опора на неизменную структуру потребления при расчете агрегатного индекса цен также обусловила применение формулы Ласпейреса при расчете индекса потребительских цен (ИПЦ), величина которого используется при индексации доходов населения.

Еще одно преимущество формулы агрегатного индекса Ласпейреса связано с возможностями перехода от ряда индексов с переменной базой сравнения к ряду индексов с постоянной базой сравнения и обратно [12, с. 548, 551].

2.2. Особенности построения индексных моделей в задачах экономического анализа

В задачах экономического анализа правильное использование общих индексов выражается в том, что индексы количественных и качественных показателей рассматриваются не изолированно, а исследуются как факторы, определяющие изменение определенного результативного показателя.

Правила построения агрегатных индексов количественных и качественных показателей связаны с обязательным важным требованием увязки индексов в систему. Это объединение позволяет реализовать индексный приём исследования на практике.

Допустим, фирма реализует один продукт. Тогда индекс выручки от реализации продукта равен произведению индекса цен и индекса физического объема продукции:

. (25)

Такой же должна быть взаимосвязь и между агрегатными индексами:

, (26)

где .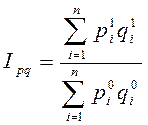

Возникает вопрос о том, какие агрегатные индексы физического объема и цен будут удовлетворять этому условию? Обратимся к табл. 9, где представлены формулы агрегатных индексов Ласпейреса и Пааше. Сопоставив варианты приведенных в таблице индексов, можно видеть, что равенство индекса стоимости произведению агрегатных индексов цен и физического объема продукции соблюдается в двух вариантах сочетания этих индексов:

1) индекса физического объема Ласпейреса и индекса цен Пааше:

, (27)

2) индекса физического объема Пааше и индекса цен Ласпейреса:

. (28)

И опять возникает проблема выбора одного из указанных вариантов. Здесь на первый план выдвигается экономическое содержание решаемых с помощью индекса задач. Так, в числителе индекса цен Пааше записана фактическая стоимость продукции отчетного периода, которая сравнивается со стоимостью фактического выпуска по базисным ценам, т. е. в случае роста цен речь идет о реальной дополнительной выручке от реализации произведенной продукции, связанной с увеличением цен производителя. Именно это обстоятельство и обусловливает выбор варианта агрегатного индекса цен Пааше. Тогда, чтобы получить индекс стоимости, агрегатный индекс физического объема должен быть рассчитан по формуле Ласпейреса.

Предпосылкой для проведения анализа в индексной форме является возможность представления результативного экономического показателя с помощью перемножения двух или более определяющих его величину показателей (факторов) или их суммирования.

Например, стоимостной объем экспорта может быть представлен в виде произведения уровня внешне торговых цен и объема экспортных поставок в натуральном выражении .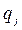

Таким образом, стоимость экспорта зависит от изменения внешнеторговых цен или объема поставок продукции в натуральном выражении либо от одновременного изменения указанных факторов. Поэтому при анализе динамики или выполнения плана по экспорту продукции необходимо показать, в какой мере изменение стоимости экспорта продукции вызвано изменением каждого из этих факторов. С экономической точки зрения небезразлично, какой из этих факторов оказал решающее влияние на увеличение объема экспорта [5, с. 366].

Оценивать роль отдельных факторов изменения результативного показателя статистика может путем построения системы взаимосвязанных индексов. Задача состоит в том, чтобы рассчитать изменение сложного показателя при изменении величины только одного фактора так, чтобы величина других факторов была сохранена на определенном постоянном уровне. В основе аналитических индексных расчетов лежит принцип элиминирования изменений величины всех факторов, кроме изучаемого. При построении индексов, оценивающих влияние отдельных факторов на изменение сложного показателя, необходимо иметь в виду, что общий результат изменения этого показателя представляет собой сумму изменения за счет влияния всех исследуемых факторов, формирующих этот показатель.

Сформулируем два дополнительных правила, позволяющих обеспечить выполнение этих условий:

1) при расчете индексов количественных показателей соизмерители принимаются на уровне базисного периода, т. е. расчет ведется по формуле Ласпейреса;

2) при расчете индексов качественных показателей веса в числителе и знаменателе фиксируются на уровне, относящемся к текущему периоду, т. е. используется формула Пааше.

Формулы агрегатных индексов позволяют разделить абсолютный прирост результативного показателя по факторам, например:

, (29)

где 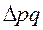– абсолютный прирост стоимости продукции;

– абсолютный прирост стоимости продукции, обусловленный изменением физического объема продукции;

– абсолютный прирост стоимости продукции, обусловленный изменением уровня цен на продукцию.

Каждая из названных величин абсолютного прироста рассчитывается как разность числителя и знаменателя соответствующего агрегатного индекса:

. (30)

▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼

▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲

Приведем формулы расчета некоторых наиболее употребляемых агрегатных индексов:

- индекс изменения общей суммы затрат на производство продукции в зависимости от объема производства q и затрат на единицу z

- индекс изменения общего фонда оплаты труда в связи с изменением численности работающих T и их средней заработной платы f

;

- индекс изменения объема продукции в связи с изменением численности работающих T и их среднего уровня выработки W

;

- индекс изменения объема продукции в связи с изменением объема основных производственных фондов Ф и показателя эффективности их использования – фондоотдачи Н

.

Аналогичным образом получают общие агрегатные индекса и по многим другим экономическим показателям.

Нетрудно заметить, что используемые в приведенных выше формулах индексы , , 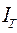получаются по методу индекса физического объема. Индексы , , , получаются по методу индекса цен.

Таким образом, рассмотренная методика распределения общего прироста товарооборота может быть полностью применима и к анализу прироста продукции, общих затрат на производство, общего фонда оплаты труда и т.д.

▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼

▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲

2.3. Сравнительный анализ с использованием территориальных индексов

Территориальные индексыпредставляют собой разновидность относительных величин сравнения, когда сопоставляются сложные показатели, относящиеся к одному и тому же периоду времени, к разным территориям (городам, районам, областям, государствам). На основе территориальных индексов выполняются международные сопоставления.

Построение простейших территориальных индексов рассмотрим на примере показателя товарооборота для двух районов А и Б. Территориальный индекс товарооборота — это отношение суммы выручки от продажи в одном из районов к аналогичному показателю в другом. Один из районов (например, Б) берется за базу сравнения, т.е.

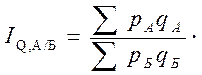(31)

Различные объёмы товарооборота обусловлены различием ассортимента и количества проданных товаров, а так же цен. Территориальный индекс физического объема товарооборота рассчитывается как

(32)

а территориальный индекс цен – как

(33)

В этих формулах:

р — средняя межрайонная цена товара каждого вида,

, (34)

q — суммарный по двум районам объем продаж каждого вида товара,

(35)

Эти сложные показатели взвешивания применяются для того, чтобы результаты расчета были обратимыми, т.е. чтобы выполнялись соотношения:

и

При этом условия индексной модели

(36)

(37)

могут нарушаться, но не очень существенно. Надо заметить, что использование такого рода территориальных индексов для анализа абсолютной разницы товарооборотов по территории дают приближенные результаты [12].